주성분 분석
차원과 차원 축소
지금까지 데이터가 가진 속성을 특성이라고 불렀는데 과일 사진의 경우 10,000개의 픽셀이 있기 때문에 10,000개의 특성이 있는 셈이다.
머신러닝에서는 이런 특성을 차원이라도 부른다. 나중에 보겠지만 이런 차원을 줄일 수 있다면 저장 공간을 크게 절약할 수 있을 것이고 차원 축소된 데이터를 지도 학습 알고리즘이나 다른 비지도 학습 알고리즘에 재사용하여 성능을 높이거나 훈련 속도를 빠르게 만들 수도 있다.
즉 이번 챕터에서 배울 내용을 미리 요약하면 그림의 10,000 개의 픽셀을 해당 이미지의 특성을 가진 몇십개의 픽셀 정보로 줄여서 그걸 가지고 다른 분야에 사용할수 있다는 것이다.
아무튼 작업을 하는 대표적인 알고리즘이 주성분 분석 (PCA)이 있다.줄여서 PCA라고도 한다.
PCA가 작동하는 원리는 책에 있는 그림으로도 잘 나와 있지만 말로 풀어쓰면 특성값들이 늘어선 주요 방향값을 찾는데 이것을 주성분 이라고 부르고 각 데이터를 이 주성분에 수직으로 투영시켜서 주성분에 포함되게 바꾼다. 여기까지의 과정을 실습해보자

과일 데이터 300개를 로드해서 PCA 클래스로 이미지를 학습시킨다. 그러면 PCA 클래스가 찾은 주성분의 크기를 출력해보면 50개의 주성분을 찾은걸 알 수 있다. 이렇게 찾은 주성분을 전 챕터에서 사용한 이미지 그리는 유틸을 이용해서 출력해보면 다음과 같다.

위의 이미지는 주성분을 찾아서 그린거고 이걸로 원본 데이터를 주성분에 투영하여 특성의 개수를 10,000개에서 50개로 줄이는 작업을 진행하자.

그럼 이렇게 데이터의 차원을 줄였다면 다시 원상 복구 할 수도 있을까? PCA 클래스는 이를 위해 inverse_transform() 이라는 메서드를 제공함.

잘 살펴보면 100% 원본이미지로 복원되지는 않았지만 그래도 잘 복원하는걸 알 수있다.
주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값을 설명된 분산이라고 하는데 PCA 클래스의 explained_variance_ratio_ 에 각 주성분의 설명된 분산 비율이 기록되어 있는데 이걸 출력해보면

50개의 분산 비율을 모두 더하면 주성분으로 표현하고 있는 총 분산 비율을 얻을수 있는데 위에서 처럼 92%가 넘는 분산을 유지하기 때문에 원본 특성을 잘 간직하고 있다는걸 알수 있다. 50개의 특성에서 분산의 비율을 그래프로 그려볼수도 있다.

그래프에서 보면 처음 10개의 주성분이 대부분의 분산을 표현하고 있다는걸 알수 있다.
그럼 이번에 이렇게 차원축소된 데이터로 지도 학습 모델을 훈련해보자.
먼저 3개의 차원 축소 하기전의 과일 사진 분류을 잘 하는지 살펴보자. 먼저 정답이 없으므로 정답지를 준비하고 로지스틱 회귀모델을 사용하여 훈련하고 교차검증 및 시간체크를 해보자.
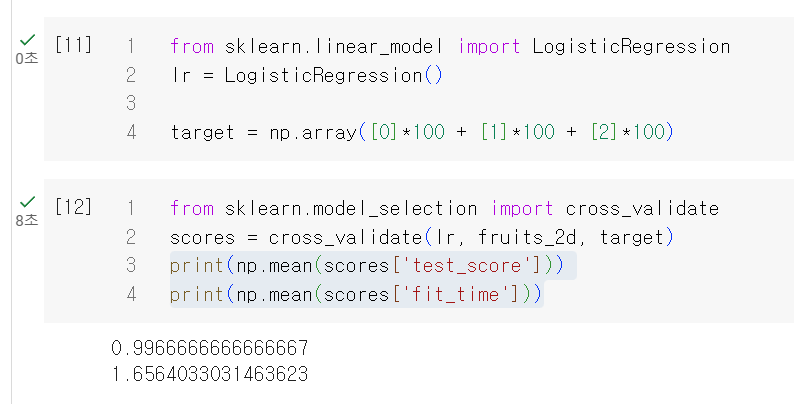
교차 검증 점수는 0.996 정도, 훈련 시간은 1.65초 정도 걸렸는데 이걸 이제 차원 축소된 데이터로 다시 해보면

정확도가 100%, 훈련시간은 0.02초로 엄청나게 차이나는걸 알 수 있다.
앞서 PCA 클래스를 사용할때 n_components 매개변수에 주성분의 개수를 지정했는데 이 대신 원하는 설명된 분산의 비율을 입력할 수도 있다. 그러면 PCA 클래스는 지정된 비율에 도달할 때까지 자동으로 주성분을 찾는다. 설명된 분산의 50%에 달하는 주성분을 찾도록 PCA 모델을 만들어보자.

단 2개네. 2개의 특성만으로 원본 데이터에 있는 분산의 50%를 표현할 수 있다.
이 모델로 원본 데이터를 변환하고 교차 검증을 해보자
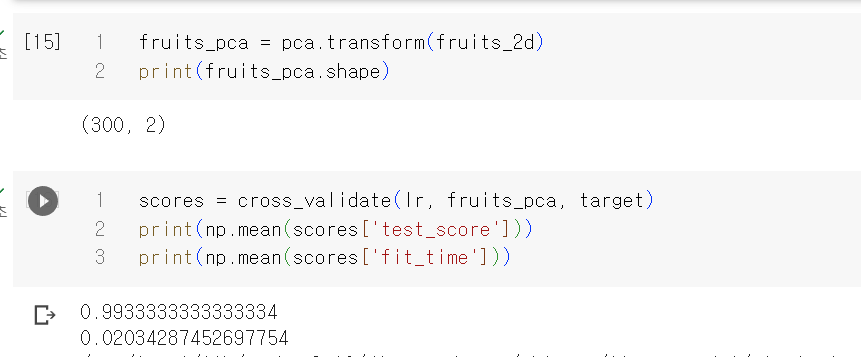
2개의 특성을 사용했을 뿐인데 99%의 정확도를 달성했다.
이번에는 차원 축소된 데이터를 사용해 k-평균 알고리즘으로 클러스터를 찾아보자.

그리고 그렇게 찾은 결과물을 보자

파이애플 라벨만 출력해 봤는데 사과 바나나만 조금 섞여있는데 나머지는 잘 분류했다. 기존 30개 특성으로 분류 한것과 별반 차이가 없다.
또 이렇게 훈련 데이터의 차원을 줄였기 때문에 3개 이하로 줄이면 그래프로 표시할 수가 있다.
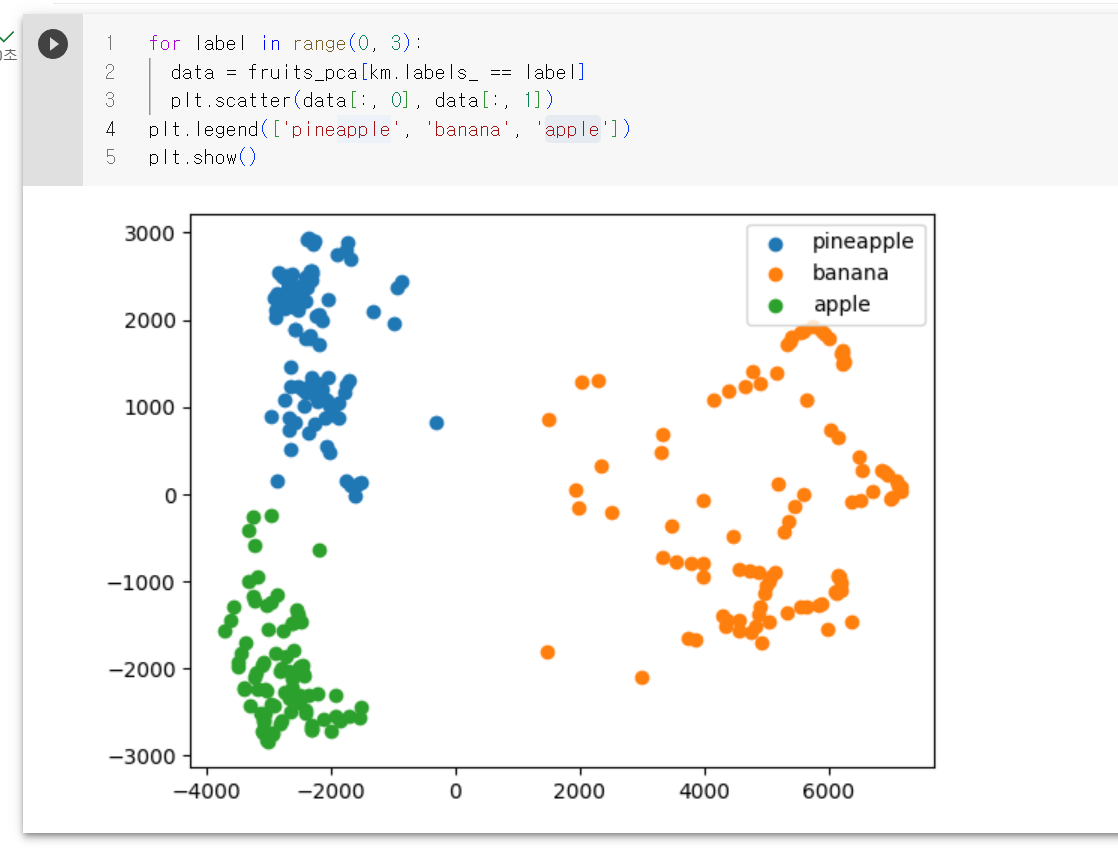
각 클러스터의 산점도가 아주 잘 구분되는걸 볼수 있다. 이 그림을 보면 사과와 파인애플 클러스터의 경계가 가깝게 붙어 있다. 이 두 클러스터의 샘플은 몇 개가 혼동을 일으키기 쉬울거 같다는 추측을 할수 있다.
참조코드
# 주성분 분석
## PCA 클래스
!wget https://bit.ly/fruits_300_data -O fruits_300.npy
import numpy as np
fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)
from sklearn.decomposition import PCA
pca = PCA(n_components=50)
pca.fit(fruits_2d)
print(pca.components_.shape)
import matplotlib.pyplot as plt
def draw_fruits(arr, ratio=1):
n = len(arr) # n은 이미지 갯수
# 한줄에 10개씩 이미지를 그린다. 샘플 개수를 10으로 나누어 전체 행 개수를 계산한다.
rows = int(np.ceil(n/10))
# 행이 1개이면 열의 개수는 샘플 개수이다. 그렇지 않으면 10개이다.
cols = n if rows < 2 else 10
fig, axs = plt.subplots(rows, cols,
figsize=(cols*ratio, rows*ratio), squeeze=False)
for i in range(rows):
for j in range(cols):
if i*10 + j < n:
axs[i, j].imshow(arr[i * 10 + j], cmap='gray_r')
axs[i, j].axis('off')
plt.show()
draw_fruits(pca.components_.reshape(-1, 100, 100))
print(fruits_2d.shape)
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)
### 원본 데이터 재구성
fruits_inverse = pca.inverse_transform(fruits_pca)
print(fruits_inverse.shape)
fruits_reconstruct = fruits_inverse.reshape(-1, 100, 100)
for start in [0, 100, 200]:
draw_fruits(fruits_reconstruct[start:start+100])
print("\n")
print(np.sum(pca.explained_variance_ratio_))
plt.plot(pca.explained_variance_ratio_)
plt.show()
### 다른 알고리즘과 함께 사용하기
### PCA로 축소한 데이터를 지도 학습에 적용해보고 차이점 알기
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
target = np.array([0]*100 + [1]*100 + [2]*100)
from sklearn.model_selection import cross_validate
scores = cross_validate(lr, fruits_2d, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
pca = PCA(n_components=0.5)
pca.fit(fruits_2d)
print(pca.n_components_)
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)
scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_pca)
print(np.unique(km.labels_, return_counts=True))
for label in range(0, 3):
draw_fruits(fruits[km.labels_ == label])
print("\n")
for label in range(0, 3):
data = fruits_pca[km.labels_ == label]
plt.scatter(data[:, 0], data[:, 1])
plt.legend(['pineapple', 'banana', 'apple'])
plt.show()
확인문제 풀이 6-3
정답 : 1번
풀이 : 1번 첫번째 주성분 - 주성분 분석은 가장 분산이 큰 방향부터 순서대로 찾으므로, 참고로 가장 큰 영향을 갖는 주성분갯수를 찾도록 따로 훈련시킬수 있음.