챕터 2-1 에서는 주어진 샘플을 훈련세트와 테스트세트로 나누어야 하는 이유와 랜덤처리를 위해 넘파이 라이브러리를 사용해봤다. 하지만 아직 데이터 입력 단계에서 할 일이 좀 더 남아있다. 사실 지금까지 한 작업은 무게와 길이의 스케일 범위가 틀리기때문에 제대로 작업한건 아니다. 그걸 맞춰가는 작업을 살펴보자.
문제 : 생선 길이, 무게로 도미 알아내기 + 수상한 도미 한마리 (2-1장에서 계속 이어짐)
(아직도 이 문제는 해결이 안됐다. ㄷㄷㄷ) 2.1에서 작업한 모델로 수상한 도미 데이터(길이25cm, 무게 150g) 한마리를 예측해보니 빙어로 나오는 문제가 발생했다. 이걸 해결해보자.
먼저 넘파이라는 효율적인 라이브러리를 배웠기 때문에 작업환경을 다시 맞춰보자.
데이터 준비

사이킷런으로 훈련 세트와 테스트 세트 나누기
2-1장에서는 데이터를 섞고 나누는걸 수동으로 처리했는데 사이킷런에는 이미 그런 작업을 도와주는 도구들이 있다.

train_test_split 이라는 도구를 이용하면 랜덤섞기, 훈련 세트와 테스트 세트 로 데이터 나누기까지 한번에 수행된다. 이렇게 처리된 테스트 데이터를 살펴보면 도미쪽으로 약간 치우친걸 알 수 있다. (3.3:1)

이건 train_test_split 에 stratify 라는 매개 변수에 타깃 데이터를 전달하면 클래스 비율에 맞게 데이터를 나눈다.

이제 테스트 세트의 비율이 원래 데이터 세트의 비율(35:14 = 2.5:1)에 비슷한 2.25:1로 맞춰진걸 알수 있다.
여기까지 기존 작업환경을 다시 세팅한것이고 수상한 도미의 데이터를 그래프로 확인해보자.

예측값은 빙어로 나와서 그래프를 찍어보면 그래프상에서는 맞는거 같다. 좀 더 체크해보자. 이 샘플의 주변데이터를 표시해보자
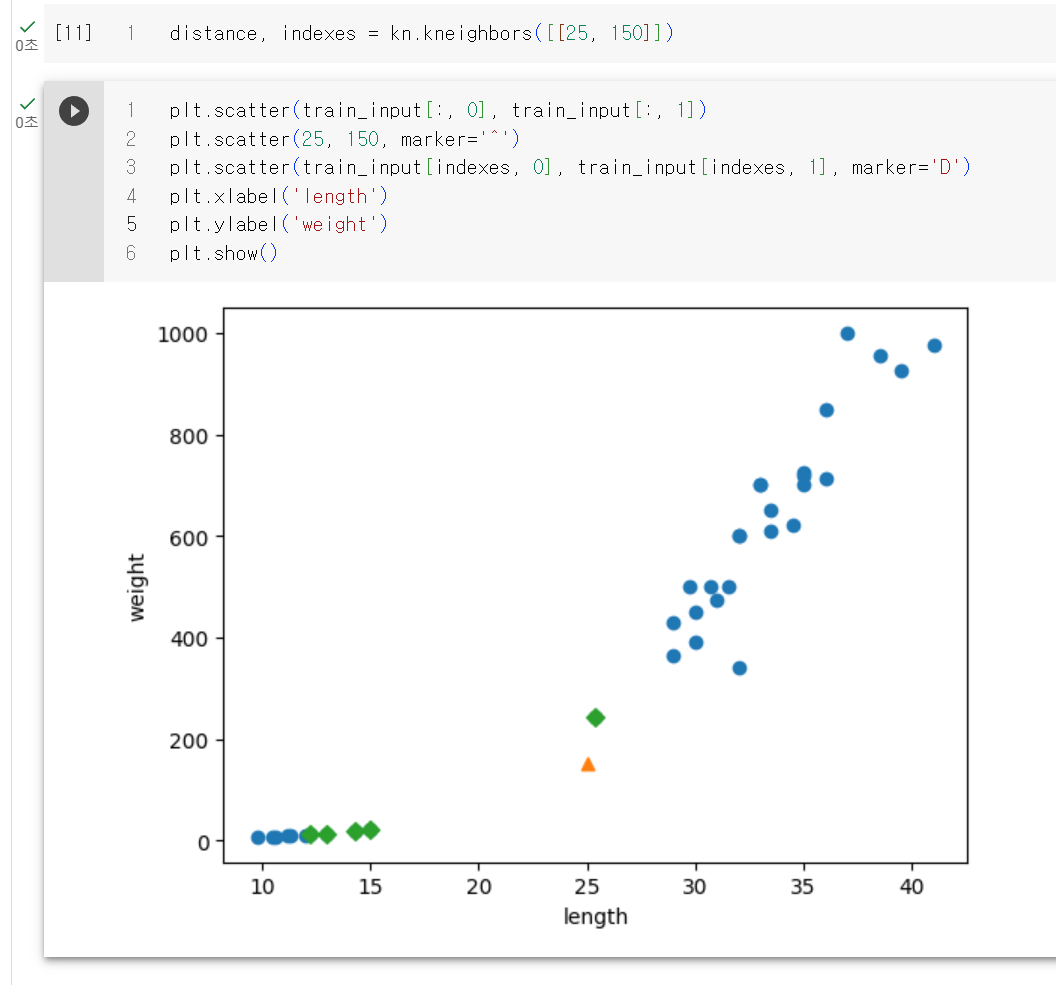
주변데이터 4개가 빙어로 표시된다. 산점도를 보면 직관적으로 도미와 가깝게 보이는데 이상하다. 책에서는 거리를 찍어보면서 답을 찾는다.
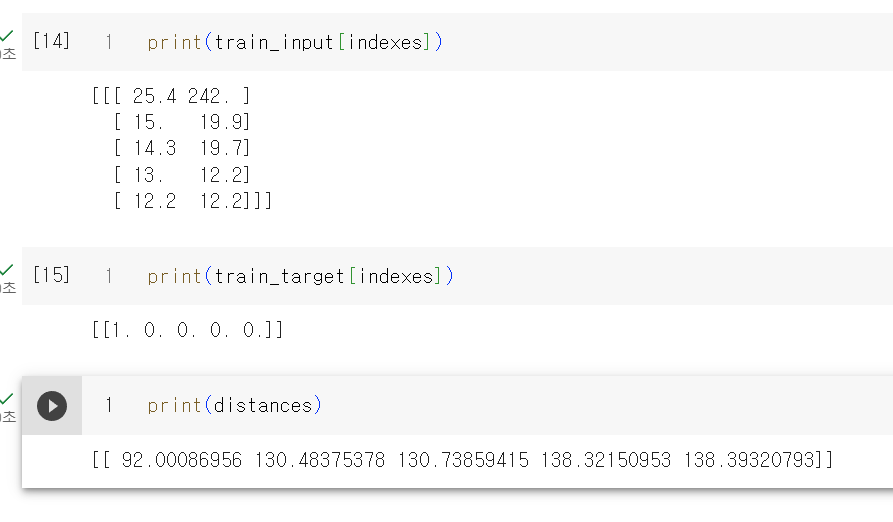
거리를 찍어보면 젤 가까운데 있는 데이터는 92, 그 다음이 130인데 직관적으로 92와 130의 차이보다는 훨씬 커 보이는걸 알수 있다. x축은 범위가 좁고 (10 ~ 40), y축은 범위가 넓어서(0, 1000) y축으로 조금만 떨어져도 아주 큰 값으로 계산되기때문이다.
그렇다고 x축의 범위를 y축만큼 늘리면 모든데이터가 수직으로 늘어서는 형태가 되었다.
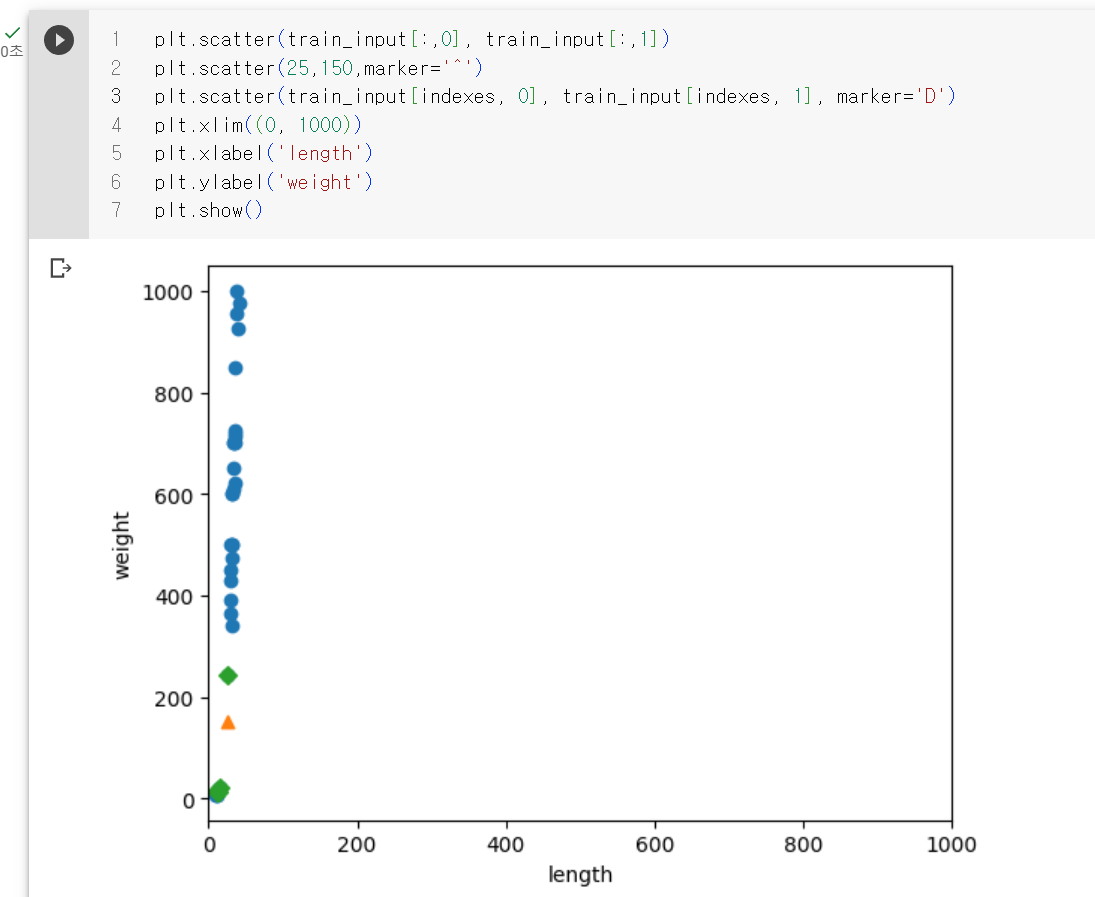
x축의 데이터(길이)는 가장 가까운 이웃을 찾는데 크게 영향을 미치지 못하는상황이다. y축의 데이터(생선의 무게)만 크게 영향을 미치게 된다.
이런 상태를 두 특성의 스케일이 다르다고 말하는데 데이터를 표현하는 기준이 다르면 알고리즘이 올바르게 예측할 수 없다. 알고리즘이 거리 기반일때 특히 그렇다.
특성값을 일정한 기준으로 맞춰주어야 하는데 이런 작업을 데이터 전처리 작업이라고 한다. 가장 널리 사용하는 전처리 방법으로는 표준점수이다.
표준점수는 각 특성값이 평균에서 표준편차의 몇 배만큼 떨어져 있는지를 나타낸다. 이를 통해 실제 특성값의 크기와 상관없이 동일한 조건으로 비교할수 있다.

이걸 코드로 표현하면 다음과 같고 바로 수상한 생선 데이터를 찍어보면 그래도 역시 이상하게 나오는데
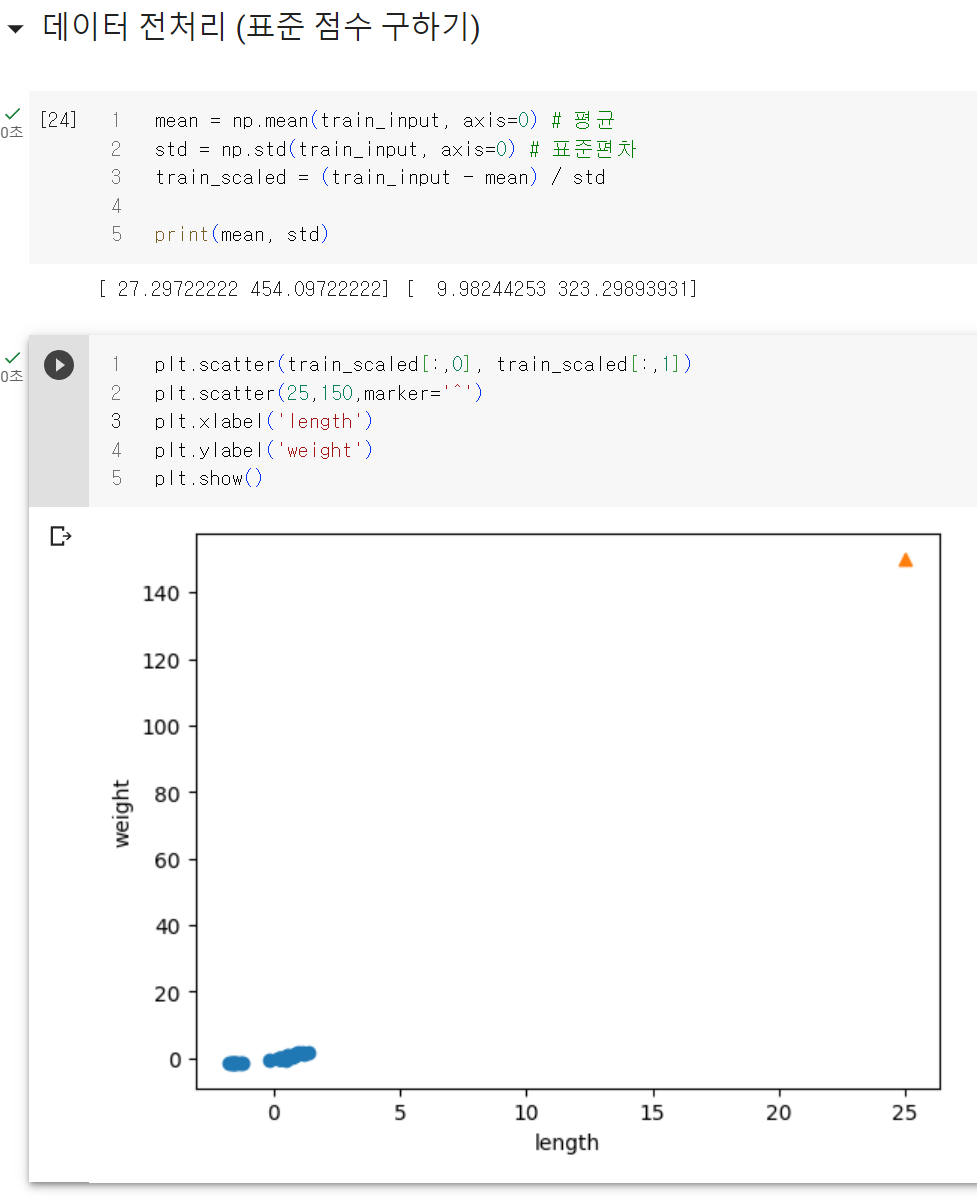
샘플 데이터 역시 동일한 비율로 변환을 안해줘서 나오는 문제였다. 이제 변환을 해서 표시하면
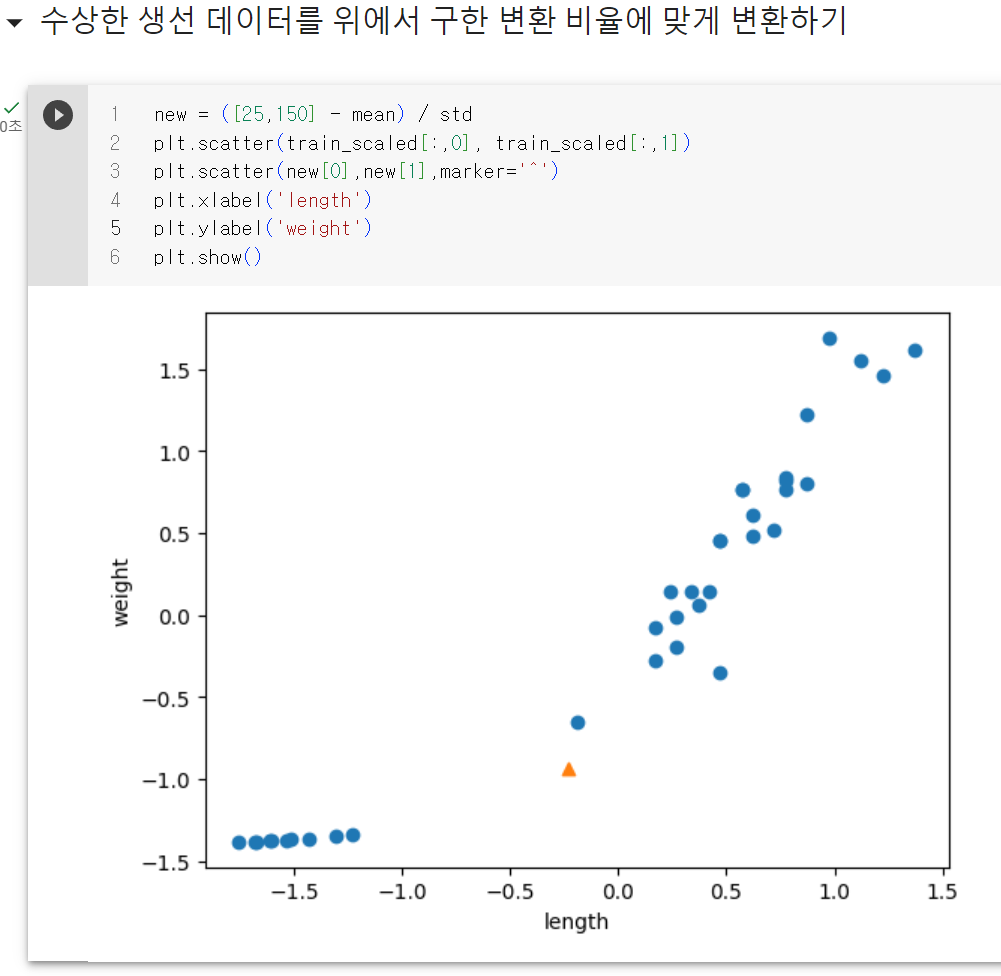
패턴은 똑같이 보이는데 달라진건 x축과 y축의 범위가 -1.5 ~ 1.5 사이로 바뀌었다는 점이다. 이제 이 데이터 셋으로 다시 훈련을 하고 테스트 데이터 역시 변환시켜서 평가를 하면 제대로 처리가 되어있는걸 알 수 있고

이제 모델이 제대로 세팅되었으니 다시 수상한 생선을 예측을 하고 그래프로 검증을 해보면
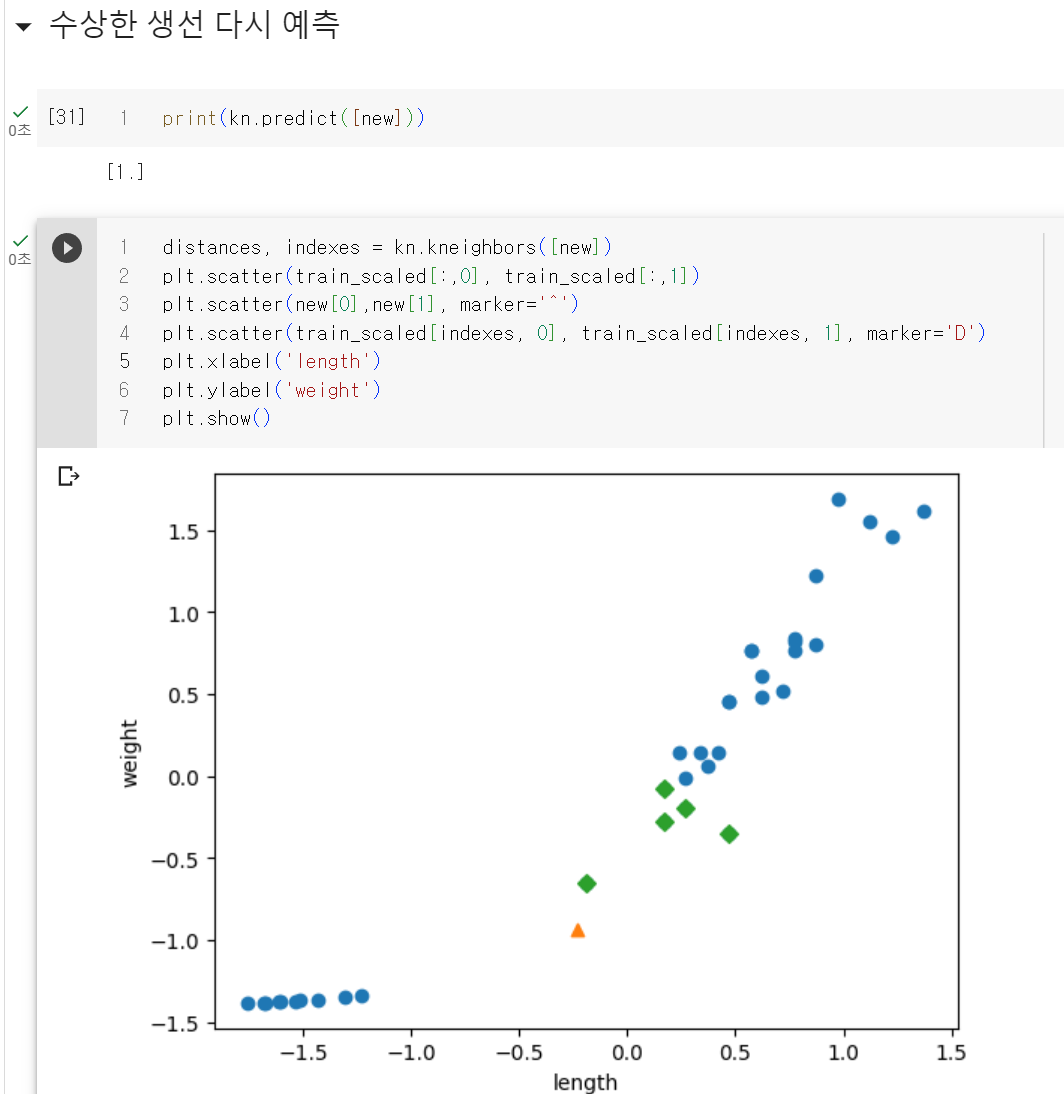
수상한 생선은 도미로 모두 제대로 처리되어 있는걸 알 수 있다
최종코드
## 생선 분류 문제3
### 데이터 전처리
fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0,
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8,
10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0,
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7,
7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
import numpy as np
np.column_stack(([1,2,3],[4,5,6]))
fish_data = np.column_stack((fish_length, fish_weight))
fish_data[:5]
fish_target = np.concatenate((np.ones(35), np.zeros(14)))
print(fish_target)
### 사이킷런으로 훈련 세트와 테스트 세트 나누기
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(fish_data, fish_target, random_state=42)
print(train_input.shape, test_input.shape)
print(train_target.shape, test_target.shape)
print(test_target)
### 클래스 비율에 맞게 다시 나누기
train_input, test_input, train_target, test_target = train_test_split(fish_data, fish_target, stratify=fish_target, random_state=42)
print(test_target)
## 수상한 도미 데이터 확인
### 기존 모델 확인
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier()
kn.fit(train_input, train_target)
kn.score(test_input, test_target)
### 수상한 도미 데이터로 예측해보기
print(kn.predict([[25,150]]))
import matplotlib.pyplot as plt
plt.scatter(train_input[:, 0], train_input[:, 1])
plt.scatter(test_input[:, 0], test_input[:, 1])
plt.scatter(25, 150, marker='^')
plt.show()
distances, indexes = kn.kneighbors([[25, 150]])
plt.scatter(train_input[:, 0], train_input[:, 1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes, 0], train_input[indexes, 1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
print(train_input[indexes])
print(train_target[indexes])
print(distances)
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25,150,marker='^')
plt.scatter(train_input[indexes, 0], train_input[indexes, 1], marker='D')
plt.xlim((0, 1000))
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
### 데이터 전처리 (표준 점수 구하기)
mean = np.mean(train_input, axis=0) # 평균
std = np.std(train_input, axis=0) # 표준편차
train_scaled = (train_input - mean) / std
print(mean, std)
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(25,150,marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
### 수상한 생선 데이터를 위에서 구한 변환 비율에 맞게 변환하기
new = ([25,150] - mean) / std
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0],new[1],marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
kn.fit(train_scaled, train_target)
test_scaled = (test_input - mean) / std
kn.score(test_scaled, test_target)
### 수상한 생선 다시 예측
print(kn.predict([new]))
distances, indexes = kn.kneighbors([new])
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0],new[1], marker='^')
plt.scatter(train_scaled[indexes, 0], train_scaled[indexes, 1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()