유니티 6가 나온것을 기점으로 다시 리마인드를 위해 다른사람들의 강좌를 따라하면서 기초 기법등을 다시 연습해볼 생각이다.
필요 프로그램 유니티 6 (60000.0.30f1)
참조 강좌 ( https://medium.com/ )
원문
https://bgolus.medium.com/the-quest-for-very-wide-outlines-ba82ed442cd9
The Quest for Very Wide Outlines
An Exploration of GPU Silhouette Rendering
bgolus.medium.com
아주 아주 좋은 블로그가 있어 해석을 하면서 나름 공부도 하는 기회로 삼을까 한다.
요점만 간추려서 적어본다. (번역글은 이탤릭체, 번역은 챗GPT)
빠른 결과만을 원하다면 여기에 누가 2022버전의 유니티로 구현해놓은 코드가 있다.
이 이야기는 실시간 렌더링에서 매우 넓은 윤곽선을 만들려고 노력한 여정에 관한 것입니다.
"나쁜" 브루트 포스 방식을 과도하게 설계하고 최적화하여 얼마나 빠르게 만들 수 있을지 실험해 본 과정입니다.
그러다 결국 처음부터 의도적으로 무시했던 방법을 받아들이게 되었습니다.
스포일러 경고:
그 방법은 바로 Jump Flood Algorithm입니다.
(점프 플러드 알고리즘 2006년 ACM에서 소개된 알고리즘이라 함)
Cracked Shell
가장 오래되고 널리 사용되는 메시(Mesh)에 윤곽선을 추가하는 방법 중 하나는 뒤집힌 외형(Inverted Hull) 방법입니다. 이 방법은 아마 3D 렌더링이 시작된 이래로 사용되어 온 기법일 것입니다. 이 방법은 메시를 두 번 렌더링하되, 두 번째 버전을 뒤집어서 안쪽으로 보이게 하고 약간 더 크게 렌더링하는 방식입니다.
이 기법의 초기 훌륭한 사례로는 Jet Set Radio를 들 수 있습니다. 이 기술은 오늘날까지도 효과적으로 사용되고 있습니다. 예를 들어, Arc System Works의 최신 3D 격투 게임들에서 이 기법을 자주 볼 수 있습니다.


약간 더 큰 메시(Mesh)를 만드는 방법은 다양하지만, 가장 일반적인 방법은 버텍스(Vertex) 노멀 방향으로 버텍스를 이동시키는 것입니다.
아주 오래된 게임에서는 이 작업이 게임 외부에서 이루어졌고, 단순히 두 개의 메시를 사용했지만, 오늘날에는 대부분 **셰이더(Shader)**를 사용하여 처리합니다.
이 메시 기반 윤곽선 스타일의 장점은 비용이 매우 적게 들고, 상대적으로 유연하며, 매우 다양한 윤곽선 두께를 표현할 수 있다는 점입니다.

메시 기반 윤곽선 시스템의 문제점은 매우 의도적인 콘텐츠 설정이 필요하다는 것입니다.
이런 설정이 없다면 갈라진 모서리(Split Edges), 구멍(Holes), 기타 시각적 결함(Artifacts)이 쉽게 발생할 수 있습니다.
저는 과거 여러 프로젝트에서 이 작업을 해본 경험이 있습니다. 필요할 경우 이 방법을 사용할 수 있다는 것은 알았지만, 콘텐츠 파이프라인과 에셋 처리에 상당한 자원을 투입했음에도 결과에 완전히 만족한 적은 없었습니다.


추가적인 작업을 해도 일관된 픽셀 단위의 완벽한 윤곽선을 얻는 것은 사실상 불가능합니다. 특히 비실시간 도구의 깔끔한 품질을 재현하려 한다면, 임의의 메시에서 이 방법은 효과적이지 않습니다. 이러한 한계를 느끼면서 저는 이 문제를 더 깊이 파고들기 시작했습니다.
...
Eh Tu Brute?
그렇다면, 오늘날 완전히 브루트 포스(Brute Force) 방식의 윤곽선 셰이더를 작성하면 어떻게 될까요?
제 컴퓨터에 탑재된 2080 Super처럼 어마어마하게 빠른 그래픽 카드에서 프레임 속도에 눈에 띌 정도로 영향을 주기 전까지 얼마나 넓은 윤곽선을 만들 수 있을까요?
이를 알아보기 위해, 저는 하나를 만들어 봤습니다.
정말 단순하고 직관적인 방법으로요.
왼쪽이 기존방식 오른쪽이 개선된 방식


꽤 괜찮아 보입니다! 사실상 포토샵에서 만든 윤곽선과 거의 동일하게 매칭됩니다.
그리고 걱정했던 것만큼 느리지도 않네요.
위 두가지 방식에 대해 유니티 URP 셰이더 그래프 책(비엘북스) 파트17에 외곽선 만들기 이론에 좀 더 자세히 나와 있다.
기본 브루트 포스 방법
다음은 코드가 수행하는 기본적인 과정을 설명한 것입니다:
- 대상 메시(또는 메시 집합)를 렌더링합니다.
- 단색 흰색 셰이더로 전체 화면의 그레이스케일 렌더 텍스처에 렌더링합니다.
- 그런 다음, 이를 다시 주 타겟에 렌더링합니다.
- 이 과정에서 셰이더가 일정 픽셀 범위 내의 모든 텍셀(texel)을 샘플링하며, **최대값(max value)**을 취합니다.
비용이 많이 드는가?
물론입니다! 하지만 일반적인 브루트 포스 윤곽선 셰이더 표준에 비춰볼 때, 제가 생각하는 꽤 넓은 윤곽선도 프레임 속도에 눈에 띄는 영향을 줄 정도로 비싸진 않았습니다.
특히 RTX 2080 Super와 1920x1080 해상도의 타겟에서 실행되는 프로토타입에서는, 이미 모든 렌더링 작업이 4ms 미만으로 처리되고 있었기 때문에 성능에 큰 영향을 주지 않았습니다.
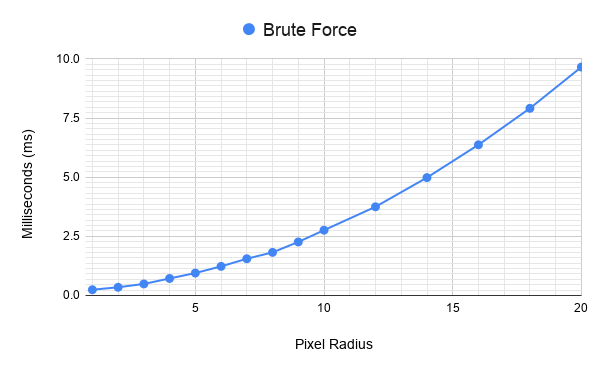
이 그래프는 전체 효과의 밀리초 비용을 보여줍니다. 여기에는 초기 실루엣 렌더 텍스처의 렌더링과 이를 **주 프레임 버퍼에 블릿(blit)**하는 과정이 포함됩니다.
너무 넓은 윤곽선은 비용이 급격히 증가
너비가 너무 넓어지면 비용이 급격히 증가합니다. 이는 셰이더가 (2 * 픽셀 반경 + 1)² 개의 샘플링을 수행하기 때문이며, 이 작업은 화면의 모든 픽셀에 대해 이루어집니다.
그래프의 선은 전형적인 O(n²) 이차 곡선을 따라가는 모습을 보이는데, 이는 이론적으로도 타당한 결과입니다.
- 반경이 20 픽셀일 때: 약 10ms에 도달했으며, 그 이상은 테스트하지 않았습니다.
- 한 번은 실수로 반경을 80으로 설정했더니 GPU가 멈춰버리는 경험을 하기도 했습니다.
실용적인 범위
- 반경 5–6 픽셀까지는 동시에 1~2개의 고유 윤곽선을 처리해야 하는 사용 사례에 대해 거의 합리적인 수준이었습니다.
- 하지만 이는 매우 넓은 윤곽선은 아니며, 컨셉 아트에서 보이는 윤곽선의 너비에는 한참 미치지 못합니다.
최적화 1단계: 메시 건너뛰기
가장 간단한 해결책은 전체 화면에 대해 작업하지 않는 것입니다. 하지만 효과를 적용할 픽셀을 어떻게 제한할 수 있을까요?
겉보기에는 "메시에서 일정 거리 이내로만 제한하면 된다"는 답이 떠오르지만, 이는 생각만큼 간단하지 않습니다.
윤곽선 셰이더 자체가 그런 작업을 수행하는 코드인데, 그런 작업을 모든 곳에서 반복하지 않으려고 하는 상황입니다!
해결책
다행히도 메시 내부 픽셀을 제외하는 쉬운 방법이 있습니다.
- **스텐실 버퍼(Stenсil Buffer)**를 사용하여 원래 메시를 렌더링합니다.
- 이 과정에서 메시 내부 픽셀만 표시(mark)합니다.
- 그런 다음 윤곽선 셰이더를 메시 내부에는 렌더링하지 않습니다.
추가 이점
- 이 방법은 **MSAA(Multi-Sample Anti-Aliasing)**가 사용될 때도 정확하게 합성되도록 만듭니다.
즉, 내부 픽셀을 제외하면서도 윤곽선 효과의 품질을 유지할 수 있습니다.

하지만 이는 카메라가 매우 가까이 줌인되지 않는 한 화면에서 큰 부분을 차지하지 않는 경우가 많습니다.
즉, 윤곽선이 적용되는 객체가 작거나 화면 밖에 있을 때, 화면에 크게 보일 때보다 더 많은 비용이 드는 문제가 발생했습니다.
이를 더 효율적으로 제한할 방법이 필요했습니다.
최적화 2단계: 외부 마스크(Exterior Mask)
CPU에서 계산된 메시 경계(bound)는 다양한 이유로 실제 메시보다 훨씬 큰 경우가 많습니다.
따라서 메시 렌더러의 경계를 기준으로 화면 내 사각형 영역을 계산하는 것은 간단하지만, 대부분의 경우 화면 전체에 가까운 크기로 계산됩니다.
메시 자체를 확장하는 방법은 이미 언급했던 문제(버텍스 확장이 브루트 포스 윤곽선의 모든 영역을 보장하지 못함)를 야기하기 때문에 적절한 해결책이 아닙니다.
다른 방법들
- 버텍스 위치를 기준으로 화면 공간의 사각형 경계 계산:
- 이론적으로 가능하지만, **스킨드 메시(Skinned Mesh)**와 함께 사용하려면 복잡해집니다.
- GPU 스키닝(GPU Skinning)을 사용하는 경우, CPU는 버텍스 위치를 알 수 없으며, 버텍스 위치를 계산 셰이더로 전달할 적절한 방법도 없습니다.
- 실루엣 렌더 텍스처의 모든 텍셀을 샘플링해 최소/최대 경계 찾기:
- 가능하지만 속도가 느리며, 결국 윤곽선이 제한될 사각형 영역만 계산할 수 있습니다.
효율적인 해결책: Mip Mapping 활용
이 문제를 해결하기 위해 Mip Mapping을 활용할 수 있다는 것을 깨달았습니다.
이는 윤곽선의 상대적 경계를 더 낮은 해상도로 계산하지만, 효율적으로 찾을 수 있는 방법입니다.
- Mip Map 생성:
- 렌더 텍스처에 대해 Mip Map을 생성합니다.
- 윤곽선 반경에 해당하는 Mip Map 레벨 샘플링:
- 윤곽선 반경을 대표하는 Mip Map 레벨을 샘플링합니다.
- 스텐실 마스크 생성:
- 이를 스텐실에 렌더링하여 윤곽선을 렌더링할 영역을 마스킹합니다.
결과
이 방법은 더 빠르며, 윤곽선을 렌더링할 영역을 효율적으로 제한할 수 있습니다.
화면 전체가 아닌 필요한 부분에만 윤곽선을 적용하도록 최적화됩니다.

저는 실제 윤곽선 너비보다 한 단계 낮은 Mip 레벨을 선택한 뒤, 마스크 셰이더에서 가변적인 너비의 1 텍셀 윤곽선을 추가로 적용하여 확장했습니다.
이 방법은 전체 Mip 레벨 단계를 사용하는 것보다 커버리지를 더 정확히 제한하는 데 도움이 됩니다.
특히, Mip Map의 해상도가 더 거칠기 때문에 확장이 실제 윤곽선보다 과장되어 보이는 문제를 완화할 수 있습니다.
성과
이 방식으로 속도가 대폭 빨라졌습니다.
- 3 픽셀 반경 이상의 윤곽선: 프레임 비용이 50% 감소했습니다.
- 20 픽셀 반경 윤곽선: 프레임 비용이 거의 75% 감소했습니다.
그러나 아직 더 개선 가능
이 방법으로 성능이 크게 향상되었지만, 더 개선할 여지가 남아 있습니다.
최적화 3단계: 윤곽선 내부 마스크(Line Interior Mask)
Mip 맵 렌더 텍스처를 사용해 대략적인 윤곽선 외부를 찾는 과정에서, 수학적으로 실수를 하여 잘못된 Mip 레벨을 샘플링하게 되었습니다. 그런데 이 과정에서 윤곽선 내부 영역을 계산하는 데도 사용할 수 있음을 깨달았습니다.
내부 마스크의 복잡성
내부 마스크는 외부 마스크보다 약간 더 복잡합니다.
- 윤곽선 원(circle)의 내부에만 해당하는 Mip 맵을 사용해야 하므로, 계산이 더 정교해야 합니다.
- 추가로 텍스처를 샘플링하여 4개의 샘플로 윤곽선을 확장하는 셰이더를 사용해 내부를 좀 더 채웁니다.
이 과정은 외부 마스크에서 1 텍셀 윤곽선을 확장하는 방식과 유사하지만, 반경의 내부에 맞춰야 하기 때문에 훨씬 더 보수적으로 작동해야 합니다.
효율성을 고려한 적용
- 윤곽선 너비가 일정 이하일 경우, 이 과정을 수행하지 않습니다.
- 이 경우, 기존 셰이더를 사용하는 것과 비용 면에서 큰 차이가 없기 때문입니다.
결론
이 방법은 윤곽선 내부 영역을 더 정확히 제한할 수 있게 해주며, 필요 이상의 렌더링 작업을 줄이는 데 도움을 줍니다.
하지만 윤곽선이 좁을 때는 효과가 크지 않아 적절히 조건을 설정해야 합니다.

이 방법은 반경 10픽셀 이상의 윤곽선에서만 실제로 효과를 발휘합니다.
- 한 자리 수 픽셀 윤곽선의 경우 비용이 최대 50% 증가했기 때문에, 반경이 이보다 작은 경우에는 이 기능을 비활성화합니다.
현재 상태
이 시점에서, 브루트 포스 윤곽선 셰이더가 실행되어야 할 영역을 저렴하게 제한할 수 있는 거의 모든 작업을 완료했습니다.
하지만 이제는 윤곽선 셰이더 자체에 주목해야 한다고 느꼈습니다.
최적화 단계 4: 반경 바깥의 샘플을 건너뛰기
원래 쉐이더에서는 텍셀(텍스처 픽셀)의 정사각형 영역을 샘플링한 후, 샘플을 원의 가장자리까지의 거리로 곱하여 안티-에일리어싱된 원을 생성했습니다. 여기서 처음 시도해본 것 중 하나는 조건문(분기)을 추가하여 원 반경 바깥의 샘플을 완전히 건너뛰는 것이었습니다. 놀랍게도, 이 방법이 효과가 있었습니다! 엄청난 성능 향상은 아니지만 약 10% 정도 더 빨라졌으며, 이것도 성과라고 할 수 있습니다.
실패한 최적화 시도 1: Early Out
샘플 박스 안에 있지만 반경 밖에 있는 샘플 위치를 이미 건너뛰도록 설정한 상태에서, 추가적으로 최댓값 샘플이 이미 1에 도달했을 경우 조기 종료(Early Out)를 위한 분기를 추가했습니다. 스텐실 마스크를 사용하지 않을 때, 이 최적화는 전체적으로 효과를 약간 느리게 만들었습니다. 왜냐하면 메시 범위 밖에 있는 픽셀도 이 추가 분기로 인한 비용을 지불하게 되지만, 실제로는 아무런 이득도 없기 때문입니다. 이렇게 되면, 메시 범위 안에 있는 픽셀에서 얻을 수 있는 잠재적 성능 향상이 상쇄됩니다.
하지만 스텐실 최적화로 쉐이더가 실행되는 영역을 메시 가까운 곳으로 대부분 제한한 후에는 이 문제가 사라졌습니다. 그래서 조기 종료 분기를 다시 추가했는데... 결과적으로 전혀 빨라지지 않았습니다. 추가 샘플을 건너뛰면서 얻을 수 있는 이점이 분기로 인해 발생하는 비용을 상쇄하지 못했습니다.
제가 이 최적화가 전반적으로 효과적이지 않았던 이유를 추측해보면, 분기 자체의 비용이 전혀 없었던 것은 아니지만, 그보다도 GPU에서 발생한 **높은 다이버전스(divergence)**가 더 큰 요인으로 작용했을 가능성이 있습니다. 간단히 말하면, 각 픽셀의 쉐이더 호출이 서로 다른 지점에서 종료되기 때문에 GPU가 이 최적화를 효율적으로 처리하지 못한 것입니다. GPU는 픽셀 쉐이더를 배치(batch) 단위로 실행하며, 배치 내 모든 호출은 가장 비싼(오래 걸리는) 픽셀의 비용만큼 소요됩니다. 따라서 일부 픽셀이 더 저렴하게 계산되더라도, 여전히 더 비싼 픽셀이 끝날 때까지 기다려야 했습니다. 결과적으로 이러한 비용이 상쇄되어 전체 성능 향상이 없었습니다.
그래도 이 방법이 여러 배 더 느려지지는 않았습니다...!
실패한 최적화 시도 2: Mip 레벨 샘플링
내부 라인 마스킹(interior line masking)을 적용하기 전에, 외곽선 내부 처리를 위한 다른 방식을 시도했습니다. 쉐이더에서 샘플링하는 Mip 레벨을 조정하여 필요한 최소한의 Mip 맵만 사용하도록 설정해 보았습니다.
스크린 공간 앰비언트 오클루전(SSAO) 성능 최적화를 위해 Mip 레벨을 사용하는 수많은 기사를 접한 적이 있었습니다. SSAO에서의 아이디어는 중심에서 멀어질수록 더 작은 Mip 레벨을 샘플링하여 메모리 대역폭 요구를 줄이고, 품질 손실도 거의 없이 좋은 결과를 얻는 것입니다.
하지만 외곽선에서는 반대가 필요했습니다. 외곽선 가장자리에서는 최상위 Mip 레벨을 샘플링하고, 가장자리에서 멀어질수록 Mip 레벨을 낮추는 방식으로 설정해야 했습니다.
결과는 매우, 매우 느려졌습니다. 성능이 몇 배가 아니라 몇 차례의 순서로(orders of magnitude) 느려졌습니다.
왜 그랬을까?
문제는 텍스처 캐시를 완전히 엉망으로 만들어버렸기 때문입니다.
기존의 브루트 포스 방식은 대부분의 텍스처 읽기가 이미 캐시에 있는 데이터를 재사용하도록 동작했습니다. 그러나 샘플 간에 Mip 레벨을 바꾸는 것은 캐시를 무효화(invalidate)시켜 효율이 급격히 떨어졌습니다.
이 방법이 SSAO에서 효과적인 이유는 SSAO가 희소 샘플링(sparse sampling)을 사용하며, 이 외곽선 쉐이더처럼 모든 데이터를 샘플링하지 않는 방식이기 때문입니다. 외곽선 쉐이더는 포괄적인 탐색(exhaustive search)을 수행해야 했기 때문에, Mip 레벨 샘플링은 오히려 성능을 크게 악화시켰습니다.
실패한 최적화 시도 3: 반경 내부 샘플 건너뛰기
Mip 맵을 이용한 내부 라인 근사 패스를 사용하고 있었기 때문에, 쉐이더에서 해당 패스가 처리할 것으로 보이는 샘플을 건너뛰는 간단한 테스트를 추가했습니다.
결과:
이 방법은 기술적으로는 더 빨랐고, 반경 외부 샘플을 건너뛰는 방식과 비슷하거나 더 나은 성능 향상을 보였습니다. 하지만 이 최적화도 반경이 큰 경우에만 유용했습니다. 특히, 반경이 너무 커서 이미 실용적이지 않은 경우에서만 효과적이었습니다.
문제점:
- 내부 채우기 스텐실(inner fill stencil)이 10픽셀 이상의 반경에서만 동작했기 때문에, 이 최적화를 적용하려면 두 가지 버전의 외곽선 쉐이더를 만들어야 했습니다.
- 하나는 내부 샘플을 건너뛰지 않는 버전.
- 다른 하나는 내부 샘플을 건너뛰는 버전.
- 또는 분기를 더 복잡하게 만들어야 했습니다. 하지만 분기를 복잡하게 만들면 성능이 저하되어 최적화의 대부분의 이점이 사라졌습니다.
결론:
쉐이더 변형(variants)을 사용하는 방식도 고려했지만, 이 최적화로 얻을 수 있는 이점이 그만한 노력이나 번거로움의 가치가 없었습니다. 그래서 결국 이 최적화 시도는 보류하게 되었습니다.
실패한 최적화 시도 4: 중첩 루프 대신 단일 루프 사용
기존 브루트 포스 방식의 쉐이더는 두 개의 루프와, 원 반경 밖의 샘플을 조기에 종료(Early Out)하는 분기를 포함하고 있었습니다. 이를 최적화하기 위해, 단일 루프를 사용하여 UV 오프셋을 루프 인덱스에서 계산하는 방법을 시도했습니다.
이 방법의 수학적 구현은 간단하며, 플립북(Flipbook) 쉐이더에서 시간(time)을 아틀라스 위치로 변환하는 것과 유사합니다.
결과:
의외로, 이 방법은 샘플링 Mip 맵을 사용한 최적화처럼 훨씬 느려졌습니다. 단일 루프를 사용하는 데 필요한 약간의 추가 ALU(산술 논리 연산) 비용이 두 개의 루프를 사용하는 것보다 약 3배 더 비쌌습니다.
다른 시도들
- SSAO 또는 보케(Bokeh) 심도 효과와 유사한 샘플 패턴 사용:
- Poisson Disc(포아송 디스크) 또는 Relaxed/Spherized Square(완화된/구형화된 정사각형) 샘플링 패턴을 사용하여 최적화를 시도.
- 결과: 이것도 느려졌습니다. 이유는 다음과 같습니다:
- 텍스처 캐시 파괴(texture cache thrashing): 캐시를 효율적으로 사용하지 못함.
- 샘플링 과잉(over-sampling): 불필요하게 많은 샘플링 발생.
- 추가 ALU 비용: 패턴 계산으로 인해 더 많은 연산 발생.
- 또한, 오버샘플링을 피하기 위해 샘플 개수를 약간 줄이면 시각적 아티팩트가 발생했습니다.
- Morton Z-Order 사용 고려:
- Morton Z-Order(지그재그 패턴)를 사용하여 샘플 순서를 최적화하는 것도 고려했지만, 결국 시도하지 않았습니다.
최종 결론
지금까지의 모든 시도에서 단순히 정사각형 영역을 한 줄씩 샘플링하고, 조기에 샘플을 건너뛰는 기존 방식보다 나은 성능을 얻지 못했습니다.
결국, 이 시점에서 새로운 방식을 포기하게 되었습니다. 추가적인 복잡한 최적화는 오히려 성능을 저하시키는 결과만 낳았기 때문입니다.
완료?
이 시점에서 결과에 꽤 만족했습니다. 반경 약 20픽셀 정도의 외곽선을 1.7ms 이하로 처리할 수 있었습니다! 이는 이미 진행 중인 다른 후처리 작업보다 적은 시간이며, 한 번에 한두 개의 객체에만 외곽선이 필요한 프로토타입에서는 충분히 빠른 성능이었습니다.
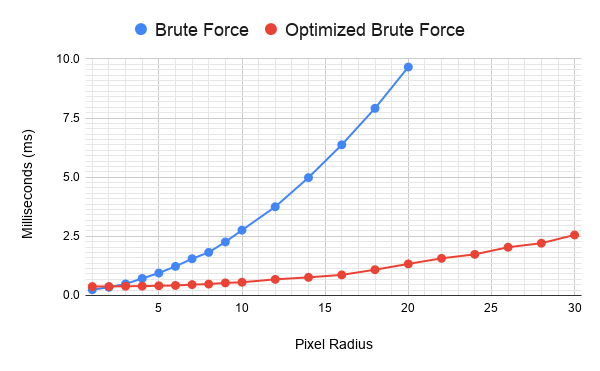
여전히 대략적으로 **O(n²)**의 이차 함수 복잡도를 가지지만, 초기의 최적화되지 않은 버전에 비해 상당히 평탄화되었습니다.

안타깝게도, 외곽선이 더 넓어질수록 Mip 맵 기반 마스크의 약점이 드러나며, 훨씬 일관성이 떨어지는 곡선을 만들어냅니다.
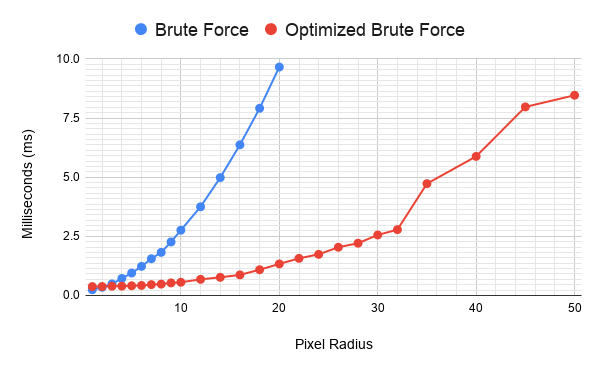


그래서 약 32픽셀 반경이 이 접근법의 한계였습니다. 더 넓은 너비에서 약간 더 복잡한 마스크를 사용하면 오히려 성능이 더 나아질 수도 있었을 것입니다. 하지만 이미 코드 자체가 매우 복잡했고, 여러 번의 패스를 거치는 방식이었기 때문에 여기에 더 많은 시간을 쓰고 싶지는 않았습니다. 대신, 과거에 사용했던 다른 접근법과 비교하기로 했습니다.
기억하겠지만, 브루트 포스(brute force) 방식이 성능 면에서 최적이 아니라는 점은 알고 있었습니다. 다만 품질 면에서는 우수한 결과를 낼 수 있었습니다. 이번 실험은 이 브루트 포스 방법을 더 빠르게 만들어, 기존의 더 일반적으로 사용되는 다른 접근법을 대체할 수 있을지 확인하는 것이 목적이었습니다.
경계 흐리기 (Blurring the Line)
외곽선을 만드는 잘 알려진 방법 중 하나는 브루트 포스 방식처럼 모든 픽셀을 일일이 검색하는 대신, **가우시안 블러(Gaussian blur)**를 활용하는 것입니다.
하지만 여기서의 핵심 질문은, 제가 복잡하게 최적화(?)된 브루트 포스 방식이 가우시안 블러 기반 방식보다 더 빠를까 하는 것이었습니다.
그래서 간단한 테스트를 설정해보았고…
블러 기반 외곽선
결과는...
아니요, 그렇지 않았습니다. 😅
결론적으로, 복잡한 브루트 포스 방식은 최적화가 되었음에도 불구하고 성능 면에서 가우시안 블러 기반 방법보다 빠르지 못했습니다.
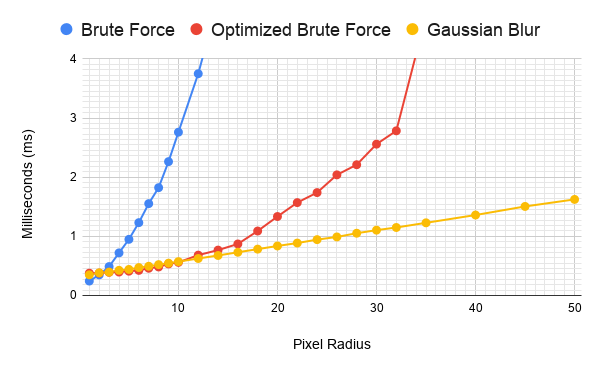

At 10 pixels or below, the optimized brute force approach was faster, for most of the range. But not meaningfully so. Blurring is clearly faster for wider radii. However not as much as I’d feared for the sub 20 pixel radius ranges I was initially playing with. Really the blur approach only became really obviously better once you got into the over 15 pixel radius range. I’d expected an inflection point where the blur would end up faster, but I was expecting it in the small single digit radii, not over 10 pixels wide. Technically 1 pixel blur based outlines were faster, but the original brute force was faster than either at that size.
10픽셀 이하의 반경에서는, 최적화된 브루트 포스 방식이 대부분의 범위에서 더 빨랐습니다. 하지만 의미 있는 차이는 아니었습니다. 반면, 더 넓은 반경에서는 블러 방식이 확실히 더 빠릅니다.
다만, 제가 처음 실험했던 20픽셀 이하의 반경에서는 예상했던 것만큼 큰 차이가 나지 않았습니다. 실제로 블러 방식이 확실히 더 나아지는 시점은 15픽셀 이상의 반경에서 나타났습니다.
저는 원래 블러 방식이 더 빠르게 되는 **전환점(inflection point)**이 훨씬 더 작은 반경, 즉 한 자릿수 픽셀 반경에서 발생할 것으로 예상했습니다. 하지만 실제로는 10픽셀 이상에서야 블러 방식이 더 유리해지기 시작했습니다.
1픽셀 블러 기반 외곽선이 기술적으로는 더 빠르긴 했지만, 그 크기에서는 원래 브루트 포스 방식이 둘 다보다 더 빠른 결과를 보였습니다.
The main strength of the blur based approach is it’s O(n). The cost increases linearly with the radius!
블러 기반 접근법의 주요 강점은 **O(n)**이라는 점입니다. 즉, 반경이 커질수록 비용이 선형적으로 증가한다는 것입니다!
And there’s still more optimization that could be had here. For a blur implementation there isn’t as easy a way to confine the area the blur ran on, so it was back to running full screen. That put it at a disadvantage to the optimized brute force. I tried some setups with attempting to reuse the existing stencil buffer from the main buffer, but Unity doesn’t make this easy so I never got that to work. I also tried creating the temporary render targets with a depth buffer to draw the stencil mask to that. The extra cost of doing that ended up completely removing any benefits it added and ended up making the blur even slower overall than the optimized brute force! Slower than the un-optimized brute force even for the first several pixel radii.
여기서도 여전히 더 많은 최적화를 시도할 여지가 있습니다. 블러 구현에서는 블러가 적용되는 영역을 쉽게 제한할 방법이 없어서 결국 전체 화면에 실행해야 했습니다. 이는 최적화된 브루트 포스 방식에 비해 불리한 점으로 작용했습니다. 기존 메인 버퍼의 스텐실 버퍼를 재사용하려고 몇 가지 설정을 시도했지만, Unity에서는 이를 쉽게 구현할 수 없었기 때문에 결국 성공하지 못했습니다. 임시 렌더 타겟을 생성하고, 여기에 깊이 버퍼(depth buffer)를 추가하여 스텐실 마스크를 그리는 방식도 시도해 보았습니다. 하지만 이 방식은 추가적인 비용이 너무 커졌고, 결국 추가된 이점이 모두 상쇄되어 블러 방식이 오히려 더 느려지는 결과를 초래했습니다. 최적화된 브루트 포스 방식보다 느려졌을 뿐만 아니라, 비최적화된 브루트 포스 방식보다도 첫 몇 픽셀 반경에서는 더 느려지는 현상이 나타났습니다. 이러한 시도들은 결과적으로 블러 방식의 효율성을 높이기는커녕 오히려 성능을 떨어뜨리는 결과를 낳았습니다.
I could confine the area to the approximate rectangular screen bounds of the mesh. But an easier optimization is to down sample the image before blurring. This makes this technique much faster that either brute force past the first few pixel range. Depending on how much down sampling you wanted to do you can roughly halve or better the cost of the wider outlines. I’m also calculating the blur kernel in the shader, and I could probably optimize the blur some more by calculating that in c# before hand.
메시의 대략적인 화면 사각형 경계로 영역을 제한할 수 있었습니다. 하지만 더 간단한 최적화 방법은 블러를 적용하기 전에 이미지를 다운샘플링하는 것이었습니다. 이 방법은 몇 픽셀 범위를 넘어서면서부터는 브루트 포스 방식보다 훨씬 빠르게 만듭니다. 다운샘플링의 정도에 따라 넓은 외곽선의 비용을 대략 절반 이하로 줄이거나 더 효율적으로 만들 수 있습니다. 현재 블러 커널(blur kernel)을 셰이더 내에서 계산하고 있는데, 이를 미리 C#에서 계산하도록 변경하면 블러를 더 최적화할 수 있을 것으로 보입니다.
But I’m not going to do that. This was really meant as a test to see if I could get the a Brute Force approach faster than a Gaussian blur outline implementation than to see how well optimized I could get the later.
하지만 그렇게 하지는 않을 것입니다. 이 실험의 진짜 목적은 가우시안 블러 외곽선 구현보다 브루트 포스 접근법을 더 빠르게 만들 수 있는지를 확인하는 것이었지, 후자의 방식을 얼마나 최적화할 수 있는지를 확인하는 것은 아니었기 때문입니다.
Because this technique also has a few problems that aren’t easily solvable.
왜냐하면 이 기술은 쉽게 해결할 수 없는 몇 가지 문제들도 가지고 있기 때문입니다.
오른쪽이 가우시안 블러 적용한 이미지


Thin, sharp, or small features can disappear or fade, the outline isn’t as precise, and proper anti-aliasing is harder. The first two are because it’s a blur. The last problem is because you have to use a separable Gaussian blur which results in an non-linear falloff, and it’s a blur. Knowing how much to sharpen a variable width edge is difficult. Adding down sampling to improve performance makes all of the above problems worse. I knew about these before which is why I’d avoided it to begin with.
얇고 날카롭거나 작은 특징들은 사라지거나 희미해질 수 있으며, 아웃라인이 정확하지 않고 적절한 안티앨리어싱을 적용하기도 어렵습니다. 첫 번째와 두 번째 문제는 블러 자체 때문입니다. 마지막 문제는 분리 가능한 가우시안 블러를 사용해야 하기 때문에 발생하며, 이로 인해 비선형적인 감쇠(falloff)가 생기고 블러 자체로 인해 문제가 됩니다. 가변 폭의 엣지를 얼마나 선명하게 해야 하는지 판단하는 것도 어렵습니다. 성능을 개선하기 위해 다운샘플링을 추가하면 위에서 언급된 모든 문제가 더욱 악화됩니다. 이런 문제들을 이미 알고 있었기에 처음부터 이를 피하려고 했습니다.

If you want a fuzzy glow, it’s great! If you want an outline that’s wide and are okay with it being rounded, it’s great! Like I mentioned earlier, I’ve used this before and it’s fast and effective for those use cases.
만약 부드러운 글로우 효과를 원한다면, 가우시안 블러는 훌륭합니다! 넓고 둥근 모양의 아웃라인을 원한다면 역시 좋은 선택입니다! 앞서 언급했듯이, 저도 이전에 이런 용도로 사용해 본 적이 있으며, 이 경우 빠르고 효과적입니다.
If you want something that competes with Photoshop’s outline quality and works well on thin edges, it’s just no where near as good as brute force.
포토샵의 아웃라인 품질과 경쟁하면서 얇은 엣지에서도 잘 작동하는 것을 원한다면, 가우시안 블러는 브루트 포스 방식에 비해 품질이 크게 떨어집니다.
At this point I was still happy enough with the optimized brute force approach that I figured that was it. Worse case I could swap to the Gaussian blur wider lines, and back to brute force the rest of the time.
이 시점에서 저는 최적화된 브루트 포스 접근 방식에 충분히 만족했고, 그것으로 결론을 내렸습니다. 최악의 경우에는 가우시안 블러를 사용해 더 넓은 라인을 처리하고, 나머지 시간에는 다시 브루트 포스를 사용할 수 있다고 생각했습니다.
I posted a bit about my journey on Twitter, thinking I’d done all I could.
저는 제가 할 수 있는 모든 것을 다 했다고 생각하며, 제 여정을 트위터에 조금 올렸습니다.
And then someone said: “What about JFA?”
그리고 누군가가 이렇게 말했습니다: “JFA는 어때요?”
Missing the Jump
중요한 단계를 놓치다.
Frell.
젠장
I’d known about the jump flood algorithm for a while, and had some experience using the results of someone else’s implementation. I’d not been impressed with the quality and didn’t think it’d work for my use case. Mainly because I didn’t think it’d work well with my self imposed requirement of handling an anti-aliased starting buffer.
저는 점프 플러드 알고리즘(Jump Flood Algorithm, JFA)에 대해 오래전부터 알고 있었고, 다른 사람이 구현한 결과물을 사용해본 경험도 있었습니다. 하지만 그 품질에 큰 감명을 받지 못했고, 제 사용 사례에 적합하지 않을 거라고 생각했습니다. 주된 이유는 안티앨리어싱된 초기 버퍼를 처리해야 한다는 제 자신만의 조건과 잘 맞지 않을 것 같았기 때문입니다.
The reality is I just didn’t understand how it worked well enough and was scared of it. Luckily I decided to try to take the time to understand it. These links helped.
사실은 제가 JFA가 어떻게 작동하는지 충분히 이해하지 못했고, 그것이 두려웠던 것이었습니다. 다행히도 시간을 들여 이해하려고 노력하기로 결심했습니다. 아래 링크들이 큰 도움이 되었습니다.
X의 Johnathon Selstad님(@makeshifted)
@bgolus @Builderboy2005, a coworker of mine, wrote a per-pixel Signed Distance Field effect that can do the whole screen at 1080p in 0.5ms with Jump Flooding. It also stores X and Y distances independently for potential gradient based effects. https://t.co
x.com
Jump Flood Algorithm
점프 플러드 알고리즘 (Jump Flood Algorithm, JFA)
This is much faster for the wide outlines, and looks just as good as brute force.
이 방법은 넓은 아웃라인 처리에 훨씬 빠르며, 브루트 포스와 동일한 수준의 품질을 제공합니다.

Once I understood the technique better I understood that. But this is still felt like a fairly complicated technique with multiple expensive passes. Surely there must be some point where the optimized brute force and blur were faster, right?
이 기술을 더 잘 이해하고 나니 그 점을 알게 되었습니다. 하지만 여전히 이 기술은 여러 번의 고비용 패스를 요구하는 비교적 복잡한 방법처럼 느껴졌습니다. 최적화된 브루트 포스와 블러 방식이 더 빠른 지점이 분명히 있어야 하지 않을까요?
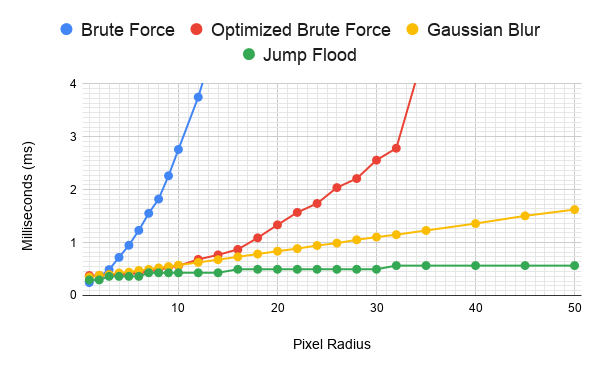
Nope.
아니요.
Ok, at 1 pixel the un-optimized brute force is faster than all of the options. But at every other radius the Jump Flood is straight up faster. A heavily hand optimized single pixel outline shader that could be nearly half as expensive as the dynamic brute force shader is. But a one pixel outline isn’t the goal here.
1픽셀에서는 최적화되지 않은 브루트 포스가 모든 옵션보다 빠르긴 합니다. 하지만 그 외의 모든 반경에서는 점프 플러드 알고리즘(JFA)이 훨씬 빠릅니다. 손으로 세심하게 최적화된 1픽셀 아웃라인 셰이더가 동적 브루트 포스 셰이더보다 비용을 거의 절반으로 줄일 수 있을지 모르지만, 여기서 목표는 1픽셀 아웃라인이 아닙니다.
The real magic of JFA is how inexpensive it is at really ridiculously wide outlines.
JFA의 진정한 마법은 엄청나게 넓은 아웃라인에서도 비용이 놀라울 정도로 낮다는 점에 있습니다.

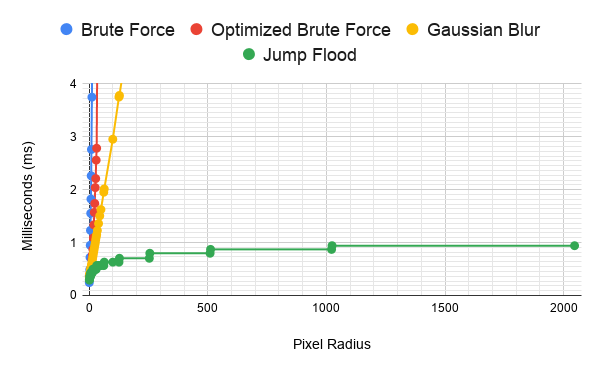
Yes, that’s a chart that goes past a 2000 pixel radius. Full screen 1080p outlines for less than 1 ms. Even full screen outlines at an 8k resolution could be just slightly over 1 ms, ignoring the extra costs from memory bandwidth increases (hint: it’ll be a lot more than 1 ms). Unlike the brute force methods, which are O(n²), or the blur which is O(n), jump flood is O(⌈log₂ n⌉). That means the cost of the outline is constant for each power of 2 pixel radius. Like the Gaussian blur, I’m not doing any limiting, apart from how many jump flood passes I do, so this is always working full screen, and it’s still this fast.
맞습니다, 이 차트는 반경 2000픽셀 이상까지를 다룹니다. 1080p 풀스크린 아웃라인을 1ms 미만으로 처리할 수 있습니다. 심지어 8K 해상도에서도 풀스크린 아웃라인은 메모리 대역폭 증가로 인한 추가 비용을 제외하면 1ms를 약간 넘는 수준일 것입니다(힌트: 메모리 대역폭 문제로 실제로는 훨씬 더 걸릴 가능성이 큽니다).
브루트 포스 방식은 **O(n²)**이고, 블러는 **O(n)**인데 비해, 점프 플러드 알고리즘(JFA)은 **O(⌈log₂ n⌉)**입니다. 이는 픽셀 반경이 2의 제곱수로 증가할 때마다 비용이 일정하다는 뜻입니다.
가우시안 블러와 마찬가지로 제가 적용한 제한은 점프 플러드 패스 횟수뿐이며, 항상 풀스크린으로 작동하도록 설정했습니다. 그런데도 이렇게 빠릅니다.
Now these are properly wide outlines.
이제야 제대로 된 넓은 아웃라인을 구현할 수 있게 되었습니다.
여기까지가 저자가 생각한 기본 이론들을 점검해본 것이고 결론은 JFA가 좋은걸 알고 그걸 적극적으로 구현하려는 과정이 아래 과정이다.
With These Three Easy Steps…
이 세 가지 간단한 단계로...
I mentioned before I didn’t think JFA would work well with my self imposed requirement of supporting anti-aliasing. And to some degree that’s still an issue, but I found a way to support anti-aliasing about as well as brute force. It’s actually better than brute force at handling thin or sharp edges, and certainly better than the Gaussian blur.
이전에 JFA(점프 플러드 알고리즘)가 안티앨리어싱을 지원해야 한다는 저의 자체 요구 사항과 잘 맞지 않을 것 같다고 말씀드렸습니다. 여전히 어느 정도 문제가 되지만, 브루트 포스와 거의 비슷한 수준으로 안티앨리어싱을 지원하는 방법을 찾았습니다. 얇거나 날카로운 가장자리를 처리하는 데 있어서는 브루트 포스보다 실제로 더 나은 성능을 보이며, Gaussian 블러보다는 확실히 더 좋습니다.
Before I go into that I want to talk a little about JFA in more detail, and the main stages of it for producing the outline. The links I posted above do a good job talking about the jump flood algorithm. If you’ve already looked at this, this might be retreading some info for you, but it’ll be important later.
그 내용을 다루기 전에 JFA에 대해 조금 더 자세히 이야기하고, 외곽선을 생성하는 주요 단계를 설명하고자 합니다. 제가 위에 올린 링크는 점프 플러드 알고리즘에 대해 잘 설명하고 있습니다. 이미 보셨다면 익숙한 정보일 수 있지만, 이후 내용을 이해하는 데 중요합니다.
The start for all of the outline techniques I tried is the same. I render out a greyscale mask of the meshes I want to have an outline. There are many possible ways to do this, but in my case I use a command buffer that renders each object with a solid white unlit material into a GraphicsFormat.R8_UNorm (aka RenderTextureFormat.R8) render texture. This is my starting mask I draw the outline from.
제가 시도한 모든 외곽선 기술의 시작은 동일합니다. 외곽선을 추가하려는 메시(mesh)의 그레이스케일 마스크를 렌더링합니다. 이를 수행하는 방법은 여러 가지가 있지만, 제 경우에는 명령 버퍼를 사용하여 각 오브젝트를 GraphicsFormat.R8_UNorm(즉, RenderTextureFormat.R8) 렌더 텍스처로 단색 흰색 비조명 머티리얼로 렌더링합니다. 이것이 제가 외곽선을 그리기 위해 사용하는 시작 마스크입니다.

Step 1: Collect Underpants
1단계: 속옷 모으기
The first stage of JFA is the initialization shader pass. This takes the mask and outputs each valid texel’s screen space or UV position. For something like a black & white mask, any texels over some value threshold, like 0.5, output their position. Any values under the threshold output some other value that’s intended as a “no position” value, or some position well outside of the plausible range. In my case I output -1.0.
JFA(점프 플러드 알고리즘)의 첫 번째 단계는 초기화 셰이더 패스입니다. 이 단계에서는 마스크를 받아서 각 유효한 텍셀(texel)의 화면 공간 또는 UV 위치를 출력합니다. 흑백 마스크 같은 경우, 0.5와 같은 값 임계치를 초과하는 텍셀들은 자신의 위치를 출력합니다. 임계치보다 낮은 값들은 "위치 없음(no position)" 값을 출력하거나, 가능 범위를 훨씬 벗어나는 위치를 출력하도록 설정합니다. 제 경우에는 -1.0을 출력하도록 설정했습니다.

Step 2: ???
2단계: ???
The second stage of JFA is the actual jump flooding pass. This shader pass samples 9 texels in a grid and gets the distance from the invoking pixel to the position stored in each of those 9 texels, then outputs the value of the closest one. This pass is run multiple times between two render textures with the spacing of the grid changing between each pass, depending on the pixel range you need.
For example, if I wanted a 14 pixel outline, I’d need 4 passes with the first run using a 8 pixel spacing, the second using an 4 pixel, third using 2, and fourth using 1. The end result is a render texture where each texel holds the value of the closest position output by the original init shader pass within the range of the largest grid sample spacing. That starting wide spacing is where the “jump” of the jump flood gets its name.
FA의 두 번째 단계는 실제로 점프 플러딩(Jump Flooding)을 수행하는 패스입니다. 이 셰이더 패스는 그리드 내 9개의 텍셀(texel)을 샘플링하여 호출한 픽셀에서 각 텍셀에 저장된 위치까지의 거리를 계산한 뒤, 가장 가까운 값의 위치를 출력합니다. 이 과정은 두 개의 렌더 텍스처 사이에서 여러 번 반복 실행되며, 그리드의 간격은 각 패스마다 변경됩니다. 이 간격은 원하는 픽셀 범위에 따라 결정됩니다.
예를 들어, 14픽셀 두께의 외곽선을 만들고 싶다면 4번의 패스가 필요합니다. 첫 번째 패스는 8픽셀 간격, 두 번째는 4픽셀 간격, 세 번째는 2픽셀 간격, 마지막 네 번째는 1픽셀 간격으로 실행됩니다. 최종적으로 생성된 렌더 텍스처는 각 텍셀이 초기화 셰이더 패스에서 출력된 위치 중, 가장 넓은 그리드 샘플 간격 내에서 가장 가까운 위치 값을 보유하게 됩니다. 이 초기 넓은 간격이 바로 점프 플러드(Jump Flood)에서 "점프"라는 이름이 유래한 부분입니다.
This can be seen a little easier if the init pass only outputs the edge.
초기화 패스가 단순히 외곽선(edge)만 출력하도록 설정하면 이 과정을 더 쉽게 시각화할 수 있습니다.

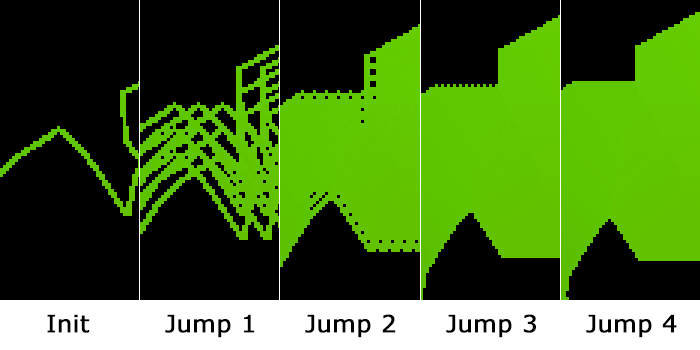


Final Jump Flood Pass Output for a 14 Pixel Radius, and 500 Pixel Radius
And yes, outputting only the edge in the init pass still produces correct results. And could be used to do both an interior, exterior, or centered line if so wanted. Some of the links I posted above show examples of just that. But I don’t need that. I only want an exterior line. Plus the outline version of the init shader is slower.
그리고 그렇습니다. 초기화 패스에서 외곽선(edge)만 출력해도 여전히 올바른 결과를 얻을 수 있습니다. 이를 활용하면 내부선, 외부선, 또는 중심에 위치한 선을 그릴 수도 있습니다. 제가 이전에 공유한 링크 중 일부에서는 이러한 예시를 보여주고 있습니다. 하지만 저에게는 그런 기능이 필요 없습니다. 저는 오직 외부선(exterior line)만 원합니다. 게다가 초기화 셰이더에서 외곽선 버전을 사용하는 것은 처리 속도가 더 느립니다.
Step 3: Profit!
3단계: 이익 실현!
The third and final pass takes the output of the second stage and gets the distance from the current pixel to the stored closest position. From that I can just use the target outline width to figure out the color that pixel should be. I.E.: if it’s less than the outline width, output the outline color, otherwise output a transparent value.
세 번째이자 마지막 패스에서는 두 번째 단계의 출력을 가져와 현재 픽셀에서 저장된 가장 가까운 위치까지의 거리를 계산합니다. 이 거리 값을 기반으로 목표 외곽선 두께를 사용해 해당 픽셀의 색상을 결정할 수 있습니다.
예를 들어, 계산된 거리가 외곽선 두께보다 작다면 외곽선 색상을 출력하고, 그렇지 않으면 투명 값을 출력하도록 설정합니다.

But just doing the basic jump flood outline ends up a bit jagged, with no anti-aliasing.

Anti-Aliasing
안티앨리어싱
So how do I support anti-aliasing? Well, for one the third pass doesn’t use a hard on / off for the outline color output, but I let it use the distance fade the edge by 1 pixel. That helps, but it’s not the biggest problem.
The init shader pass I mentioned above is effectively aliasing the output of the mask, so even if I render that render texture with anti-aliasing enabled, it’ll still end up having a jagged edge since that’s all the init pass is outputting.
그렇다면 어떻게 안티앨리어싱을 지원할까요? 우선, 세 번째 패스에서 외곽선 색상을 출력할 때 단순히 온/오프 방식으로 처리하지 않고, 거리 값을 활용해 외곽선을 1픽셀 정도 부드럽게 페이드(fade) 처리하도록 설정합니다. 이것만으로도 어느 정도 도움이 되지만, 가장 큰 문제는 아닙니다.
앞서 언급한 초기화 셰이더 패스는 사실상 마스크 출력 자체를 앨리어싱(계단현상)되도록 만듭니다. 그래서 렌더 텍스처에 안티앨리어싱을 활성화해도 초기화 패스에서 출력된 결과가 울퉁불퉁한 경계를 가지게 되어, 결국 최종 결과도 울퉁불퉁한 외곽선을 가지게 됩니다.

In the above example you can see some minor anti-aliasing in the step corners. That’s the anti-aliased distance fade. But that doesn’t help the edges that are almost straight with the screen vertical or horizontal. There the stair stepping is still quite obvious.
위의 예제에서 단계 모서리 부분에서 약간의 안티앨리어싱이 적용된 것을 볼 수 있습니다. 이는 안티앨리어싱 처리된 거리 페이드(distance fade) 덕분입니다. 그러나 이는 화면의 수직 또는 수평에 거의 평행한 가장자리에는 도움이 되지 않습니다. 그런 부분에서는 계단 현상(stair-stepping)이 여전히 뚜렷하게 나타납니다.
I realized I could modify the init to make a guess at where the closest sub-pixel edge was based on the anti-aliased color. The basics of this is any mask texel that’s fully black I output the “no position” value. For any mask texel that’s white I output that pixel position. The values that aren’t fully black or white are the interesting ones. For that I check the texel values immediately around the current one and compare them to find the average direction.
저는 초기화 단계에서 안티앨리어싱된 색상을 기반으로 가장 가까운 서브 픽셀(sub-pixel) 가장자리를 추정할 수 있도록 수정할 수 있다는 것을 깨달았습니다. 기본 아이디어는 마스크 텍셀 값이 완전히 검정(black)인 경우 "위치 없음(no position)" 값을 출력하는 것입니다. 마스크 텍셀이 완전히 흰색(white)일 경우 해당 픽셀의 위치를 출력합니다.
하지만 완전히 검정도 아니고 완전히 흰색도 아닌 값들이 흥미로운 부분입니다. 이러한 경우, 현재 텍셀 주변의 값을 확인하고, 이를 비교하여 평균 방향(average direction)을 계산합니다.
For sub pixel position estimation, lets just think about this on one axis to start. One thing to be mindful of here is the position being output by a basic init pass is not actually of the geometry edge, but rather half a pixel inside the geometry edge.
서브 픽셀 위치 추정을 위해, 우선 이를 한 축(1D)에서만 생각해 보겠습니다. 여기서 주의해야 할 점은, 기본 초기화 패스에서 출력되는 위치는 실제 기하학적 경계선(geometry edge)의 위치가 아니라, 기하학적 경계선 안쪽으로 반 픽셀 정도 들어간 위치라는 것입니다.
이 차이는 안티앨리어싱 처리 및 정확한 경계 추정을 위해 매우 중요한 요소로, 정확한 서브 픽셀 위치를 계산하려면 이를 고려해야 합니다.
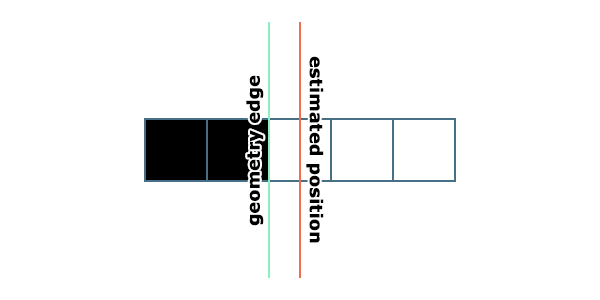
This isn’t a problem though. It actually has some benefits we can come back to later. If I have an anti-aliased mask texel with a value of 0.5, it means the geometry was covering approximately half of that pixel. But from that single texel alone you don’t know which half. But we can make a good guess. By sampling the left and right texels we can estimate which direction the closest edge is in just by subtracting the right texel’s value from the left. If the right texel is 1 and left is 0, then I know the geometry is covering the right side. And we can adjust the half pixel inset position to be half a texel in that direction.
이것은 문제가 되지 않습니다. 사실, 나중에 논의할 몇 가지 이점도 있습니다. 예를 들어, 안티앨리어싱된 마스크 텍셀 값이 0.5라면, 이는 기하학이 해당 픽셀의 약 절반을 덮고 있음을 의미합니다. 하지만 그 하나의 텍셀만으로는 어느 쪽 절반인지 알 수 없습니다. 그러나 우리는 좋은 추정을 할 수 있습니다.
왼쪽과 오른쪽 텍셀 값을 샘플링하여 가장 가까운 경계가 어느 방향에 있는지 추정할 수 있습니다. 방법은 간단히 오른쪽 텍셀 값에서 왼쪽 텍셀 값을 빼는 것입니다. 예를 들어, 오른쪽 텍셀 값이 1이고 왼쪽 텍셀 값이 0이라면, 기하학이 오른쪽 부분을 덮고 있다는 것을 알 수 있습니다. 그런 경우, 반 픽셀 정도로 안쪽으로 들어간 위치를 해당 방향으로 조정할 수 있습니다.
이를 통해 보다 정확한 서브 픽셀 위치 추정이 가능하며, 결과적으로 부드럽고 정밀한 외곽선을 생성할 수 있습니다.
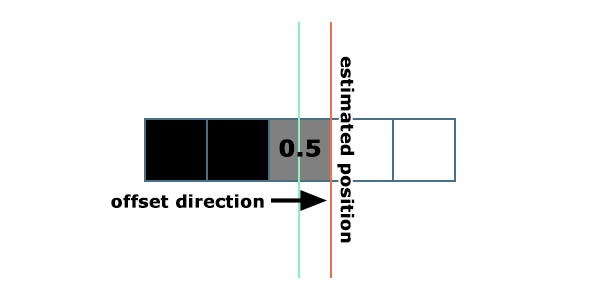
If the reverse is true then it’s covering the left side. If both the left and right values are the same, then the best guess we can make is that it’s centered on the pixel. I then do the same sampling above and below texels. This gives me a directional offset to approximate the subpixel position, which I then add to the current pixel position and output in the init pass.
반대로 오른쪽 값이 0이고 왼쪽 값이 1이라면, 기하학이 왼쪽 부분을 덮고 있다는 것을 알 수 있습니다. 만약 왼쪽과 오른쪽 값이 동일하다면, 가장 합리적인 추정은 기하학이 해당 픽셀의 중심에 위치하고 있다는 것입니다.
이 동일한 방식으로 위쪽과 아래쪽 텍셀도 샘플링합니다. 이렇게 하면 서브 픽셀 위치를 근사하기 위한 방향 오프셋(direction offset)을 얻을 수 있습니다. 그 후 이 오프셋을 현재 픽셀 위치에 더하여 초기화 패스에서 출력합니다.
이 방법은 서브 픽셀 정밀도를 높이고, 특히 경계가 부드럽게 보이도록 안티앨리어싱 품질을 크게 향상시킵니다.

This looks quite good compared to the original brute force version. However just doing the horizontal and vertical axis meant some obvious artifacts in sharp corners where a single pixel could show up. Below you can see the corner has a “bubbled” look to it compared to the brute force approach. Though that too isn’t quite right and is a little too soft and rounded.
이 방식은 원래의 브루트 포스 방식과 비교했을 때 꽤 좋은 결과를 보여줍니다. 그러나 수평 축과 수직 축만 고려했을 때, 날카로운 모서리(sharp corners)에서 명백한 아티팩트(artifact)가 나타난다는 문제가 있습니다. 예를 들어, 단일 픽셀이 보이는 "거품 모양(bubbled)" 같은 현상이 모서리 부분에 나타날 수 있습니다.
아래 예제를 보면, 모서리 부분이 브루트 포스 방식과 비교해 다소 거품처럼 둥글게 나타나는 것을 알 수 있습니다. 하지만 브루트 포스 방식도 완벽하지는 않습니다. 브루트 포스 방식은 모서리가 너무 부드럽고 둥글게 처리되기 때문에 날카로움을 잃게 됩니다.
결과적으로, 모서리의 날카로움(sharpness)을 유지하면서도 자연스러운 안티앨리어싱 처리를 위해 추가적인 조정이나 개선이 필요합니다.

This is because on single pixel corners the estimation basically thinks this is a pixel floating by itself and doesn’t do any (or enough) offsetting. So I sampled diagonals as well and add those with a slightly reduced weight. Then I normalize the resulting direction vector. If some of you are reading that and thinking “that sounds like a Sobel operator”. Yep.
문제는 단일 픽셀로 이루어진 모서리에서 추정이 이 픽셀을 "혼자 떠 있는 픽셀"로 간주하며 충분한 오프셋을 적용하지 않기 때문입니다. 이를 해결하기 위해 대각선 방향도 샘플링하여 방향 오프셋을 계산에 포함시켰습니다. 대각선 값은 약간 줄어든 가중치로 추가합니다. 그런 다음 결과 방향 벡터를 정규화(normalize)합니다.
만약 이 설명을 보고 "이거 소벨 연산자(Sobel operator) 같아 보이는데?"라고 생각했다면, 맞습니다. 이 방식은 기본적으로 소벨 연산자와 유사합니다.
이 접근법은 대각선 방향 정보를 추가로 고려하기 때문에 단일 픽셀 모서리에서 더 정확한 서브 픽셀 위치 추정을 가능하게 합니다. 결과적으로, 모서리에서 발생하는 "거품 효과(bubbled look)"를 줄이고, 더욱 자연스러운 외곽선을 생성할 수 있습니다.

I had tried a couple of different weights on the diagonal and ended up recreating Sobel on accident.
대각선 방향에 여러 가지 가중치를 적용해 보다가, 우연히 소벨 연산자(Sobel operator)를 재현하게 되었습니다.

This ends up being very close to the original brute force approach. And because of the sub pixel estimation and the fact it doesn’t fade out on anti-aliased corners, may actually be closer to the ground truth.
이 방법은 결과적으로 원래의 브루트 포스 방식과 매우 유사해집니다. 하지만 서브 픽셀 추정 덕분에, 그리고 안티앨리어싱된 모서리에서 페이드아웃(fade-out)이 발생하지 않는 점 때문에 실제에 더 가까운 결과를 얻을 수 있습니다.
Before I mentioned that having the init pass output position being half a pixel inset from the real edge, and that this was actually an advantage. The reason for that comment is imaging a line that’s only a single pixel wide, or narrower.
앞서 초기화 패스에서 출력되는 위치가 실제 경계에서 반 픽셀 정도 안쪽으로 들어가 있다는 점을 언급했었고, 이것이 실제로는 장점이라고 말씀드렸습니다. 그렇게 말한 이유는, 선(line)의 두께가 단지 한 픽셀이거나 그보다 더 얇을 때를 상상해 보면 이해할 수 있습니다.
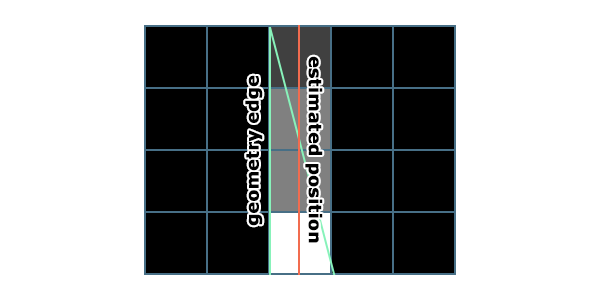
In the above example, the estimated edge doesn’t line up with the real geometry. But we can only store a single position per texel, and we can only see that single texel line. If we were attempting to store the actual edge position, in the above case there are two edges and we’d have to pick one. The result would be the nearest distance wouldn’t be centered and the outline would be wider on one side than the other. For wide edges, that probably wouldn’t be obvious. But a 1 pixel outline? That would be obvious as only one side of the line would get an outline. This is why storing a half-pixel inset position is beneficial. We can still draw a correct 1 pixel outline on a 1 pixel wide shape by using a 1.5 pixel distance. This is something even the brute force method has a hard time with.
위의 예제에서 추정된 경계는 실제 기하학적 경계와 정확히 일치하지 않습니다. 하지만 우리는 텍셀당 하나의 위치만 저장할 수 있으며, 오직 그 단일 텍셀 선(line)만 볼 수 있습니다. 만약 실제 경계 위치를 저장하려고 한다면, 위의 경우처럼 두 개의 경계가 존재하게 되고, 둘 중 하나를 선택해야 합니다. 그 결과 가장 가까운 거리가 중앙에 정렬되지 않고, 외곽선이 한쪽에서 더 넓어지게 됩니다.
넓은 외곽선이라면 이 문제가 명확히 드러나지 않을 수도 있습니다. 하지만 1픽셀 두께의 외곽선이라면, 선의 한쪽만 외곽선이 적용된다는 점이 눈에 띄게 됩니다. 이 때문에 반 픽셀 안쪽으로 삽입된 위치를 저장하는 것이 유리합니다. 이렇게 하면 1.5픽셀 거리를 사용하여 1픽셀 두께의 도형에서도 올바른 1픽셀 외곽선을 그릴 수 있습니다. 이는 브루트 포스 방식조차 처리하기 어려운 문제를 해결할 수 있는 방법입니다.

It’s not perfect. In the above image if you look closely you can see the outline fades out a little where it shouldn’t a little down from the top where it transitions from 25% coverage to 50% coverage. Doing a little more work in the init could probably fix this, but this is a rare enough scenario that I’m happy leaving it as is. I mean, it’s pretty darn good as is, and is only obvious when this zoomed in.
완벽하지는 않습니다. 위 이미지에서 자세히 보면, 외곽선이 페이드 아웃되면 안 되는 부분에서 약간 사라지는 것을 볼 수 있습니다. 이는 상단에서 약간 아래로 내려온 지점, 즉 도형의 픽셀 커버리지가 25%에서 50%로 전환되는 지점에서 발생합니다.
초기화 단계에서 약간의 추가 작업을 한다면 이 문제를 해결할 수 있을지도 모르지만, 이는 매우 드문 상황이기 때문에 현재 상태 그대로 두는 것이 만족스럽습니다. 지금 상태도 꽤 훌륭하며, 이렇게 확대해서 보지 않으면 거의 눈에 띄지 않는 수준입니다.
In comparison the brute force method just fades out entirely.
이에 비해 브루트 포스 방식은 해당 부분에서 외곽선이 완전히 사라져 버립니다.

That’s clearly wrong, even when not zoomed in.
그것은 명백히 잘못된 결과이며, 확대하지 않아도 눈에 띌 정도로 문제가 드러납니다.
Optimizations
최적화
This is already incredibly fast, but it didn’t stop me from at least attempting some further optimizations.
이 방식은 이미 매우 빠르지만, 저는 추가 최적화를 시도하는 것을 멈추지 않았습니다.
“Optimizations?”
I found only doing the diagonals and not doing a full Sobel gave very nearly identical results most situations. And it was faster! This produced a compiled shader that had roughly half as many instructions! Nice optimization right?
"최적화?"
대각선 방향만 처리하고 전체 소벨(Sobel)을 사용하지 않아도 대부분의 상황에서 거의 동일한 결과를 얻을 수 있다는 것을 발견했습니다. 게다가 이 방식은 더 빠릅니다! 이를 통해 컴파일된 셰이더는 명령어 수가 거의 절반으로 줄어들었습니다. 멋진 최적화 아닙니까?
Well, not really. It was technically faster, but trivially so. It was faster by about a single microsecond. That’s one millionth of a second faster, less than the margin of error in profiling. Less than half a percent of the effect’s cost for a single pixel radius outline. It also caused the lines to get slightly too wide on diagonal edges. So while it was faster, I still do the whole Sobel operation as it doesn’t meaningfully impact the performance. The init shader pass was also already the least expensive of the three, so this was more an attempt to squeeze water from a stone.
사실, 그렇지는 않았습니다. 기술적으로는 더 빨라졌지만, 그 차이는 미미한 수준이었습니다. 대략 1마이크로초(백만분의 1초) 정도 빨라졌을 뿐인데, 이는 프로파일링 오차 범위보다 작은 수준입니다. 단일 픽셀 반경 외곽선 효과의 비용에서 0.5%도 안 되는 차이였습니다.
게다가 이 방식은 대각선 가장자리에서 선이 약간 더 넓어지게 만드는 문제가 있었습니다. 그래서 비록 더 빠르기는 했지만, 여전히 전체 소벨 연산을 사용하기로 했습니다. 왜냐하면 성능에 실질적으로 영향을 미치지 않기 때문입니다. 초기화 셰이더 패스는 세 단계 중에서도 가장 비용이 적게 드는 부분이었기 때문에, 이번 최적화는 마치 "돌에서 물을 짜내려는 시도"에 가까웠습니다.
The jump flood passes take up most of the time, so that’d be a better place to look to optimize. And I did think of a pretty simple one here. The basic idea is you’re looking for the closest of 9 the samples by comparing the distance from the current pixel. Basically all examples you’ll find, including those I link above, use a length() call and compare the results. But you don’t need the linear distance. You can get away with the square distance, which cheaper to compute with a dot product. That removes 9 square roots from the shader, so that should be a good savings.
점프 플러드 패스가 대부분의 시간을 차지하므로, 최적화를 위해 이 부분을 집중적으로 살펴보는 것이 더 나을 것입니다. 그리고 여기서 꽤 간단한 최적화 방법을 생각해냈습니다.
기본 아이디어는 현재 픽셀에서 9개의 샘플 중 가장 가까운 샘플을 찾기 위해 거리를 비교하는 것입니다. 일반적으로, 제가 위에서 언급한 예제들을 포함해 대부분의 예제에서는 length() 함수를 호출하여 선형 거리를 계산한 후 그 결과를 비교합니다. 하지만 사실 선형 거리를 사용할 필요는 없습니다.
대신, 거리의 제곱값(square distance)을 사용해도 충분합니다. 제곱 거리 값은 선형 거리를 구하는 데 필요한 제곱근(square root) 계산을 생략할 수 있습니다. 이를 위해 점 곱(dot product)을 활용하면 더 저렴하게 계산할 수 있습니다.
이 방식은 셰이더에서 9번의 제곱근 계산을 제거하므로, 상당한 성능 향상을 기대할 수 있습니다. 이는 간단하지만 효과적인 최적화 방법입니다.
Again, nope. I could not measure a difference here at all, not even a single microsecond. More or less any kind of clever shader change I attempted here resulted in no change, or made things slower. Both of these shader passes are completely hardware texture unit limited. I still use this optimization though, because it does no harm.
다시 말하지만, 아닙니다. 여기서도 성능 차이를 전혀 측정할 수 없었습니다. 단 1마이크로초조차 차이가 나지 않았습니다. 제가 시도한 모든 "똑똑한" 셰이더 변경 방법은 아무런 변화도 가져오지 않거나, 오히려 더 느려졌습니다.
이 두 셰이더 패스는 모두 하드웨어 텍스처 유닛에 의해 완전히 제한되어 있었기 때문입니다. 하지만 이 최적화는 아무런 부정적인 영향을 미치지 않으므로 여전히 사용하고 있습니다. 최소한, 셰이더가 더 깔끔하고 논리적으로 보이기라도 하니까요. 😊
Render Texture Format
The biggest savings I got was to use a GraphicsFormat.R16G16_SFloat (aka RenderTextureFormat.RGHalf) render texture instead of a GraphicsFormat.R32G32_Sfloat (aka RenderTextureFormat.RGFloat). That reduced the memory requirements in half, but still more than enough precision. That alone dropped the cost of the init pass from 47 μs to 28 μs, and the jump flood pass from 75 μs to 67 μs. Not a lot, but for a 50 pixel radius outline the entire effect dropped from 630 μs to 565 μs. That’s at a least measurable improvement of around 65 μs, even if they’re both effectively 0.6 ms. However R16G16_SFloat had some weird precision issues, which caused the outline to be slightly offset in the subpixel position, even when not using the subpixel estimation. So I swapped to R16G16_SNorm instead, which removed the issues while still retaining the same memory footprint. This is ever so slightly slower than the R16G16_SFloat format. R16G16_UNorm also works, and is technically twice the precision for the 0.0 to 1.0 range I was using, but it requires a small amount of extra math to scale the encoded range that added about 8 μs to the same 50 pixel radius test. And you could use the R16G16_SNorm with a similar bit of extra math to get the same precision at the same relative cost increase. For 1080p, I didn’t think it was necessary.
가장 큰 성능 향상은 GraphicsFormat.R16G16_SFloat(즉, RenderTextureFormat.RGHalf) 렌더 텍스처를 사용하는 것이었습니다. 원래 사용하던 GraphicsFormat.R32G32_SFloat(즉, RenderTextureFormat.RGFloat)와 비교했을 때, 메모리 요구량이 절반으로 줄어들었지만 여전히 충분한 정밀도를 유지했습니다.
이 변경만으로 초기화 패스의 비용이 47μs에서 28μs로 줄었고, 점프 플러드 패스는 75μs에서 67μs로 줄었습니다. 큰 차이는 아니지만, 50픽셀 반경 외곽선 효과에서 전체 효과 비용이 630μs에서 565μs로 줄어들었습니다. 이는 약 65μs 정도의 눈에 띄는 개선이며, 결과적으로 두 값 모두 0.6ms 수준이긴 하지만 여전히 의미 있는 성능 향상이었습니다.
그러나 R16G16_SFloat 포맷에서는 이상한 정밀도 문제가 발생했습니다. 이는 서브 픽셀 추정을 사용하지 않을 때도 외곽선이 서브 픽셀 위치에서 약간 어긋나는 현상을 일으켰습니다. 이를 해결하기 위해 R16G16_SNorm으로 변경했으며, 메모리 사용량은 동일하면서도 이러한 문제를 해결할 수 있었습니다. 다만, R16G16_SNorm은 R16G16_SFloat보다 약간 더 느렸습니다.
R16G16_UNorm도 사용할 수 있으며, 0.0~1.0 범위에서 기술적으로 두 배의 정밀도를 제공하지만, 인코딩 범위를 스케일링하기 위한 약간의 추가 연산이 필요했습니다. 이로 인해 동일한 50픽셀 반경 테스트에서 약 8μs 정도의 추가 비용이 발생했습니다. 비슷한 방식으로 R16G16_SNorm도 추가 연산을 통해 같은 정밀도를 얻을 수 있지만, 역시 동일한 비용 증가를 초래합니다.
1080p 해상도에서는 이러한 추가 정밀도가 필요하지 않다고 판단했습니다.
Separable Axis JFA
분리 축 JFA (Separable Axis JFA)
The next optimization came in the form of an idea proposed by Alan Wolfe (aka demofox), who’s article I linked above.
다음 최적화는 **Alan Wolfe(aka demofox)**가 제안한 아이디어에서 나왔습니다. 그의 글은 제가 이전에 공유한 링크에 포함되어 있습니다.
Shadertoy
0.00 00.0 fps 0 x 0
www.shadertoy.com
This splits up each of the flood pass into two separate passes, each only doing one axis at a time. This nearly doubles the total number of passes required for the effect, but reduces the number of texture samples by a third. Amazingly it is faster! By about 35 μs total, bringing that 565 μs down to 530 μs. Honestly I have no idea if it’ll be faster on all GPUs though.
이 방법은 각 점프 플러드 패스를 두 개의 별도 패스로 나누어 한 번에 한 축만 처리하도록 합니다. 이렇게 하면 효과를 위해 필요한 패스의 총 개수가 거의 두 배로 늘어나지만, 텍스처 샘플의 개수를 3분의 1로 줄일 수 있습니다.
놀랍게도, 이 방식이 더 빠릅니다! 전체적으로 약 35μs를 절약할 수 있었으며, 이를 통해 총 실행 시간이 565μs에서 530μs로 감소했습니다.
다만, 이 방식이 모든 GPU에서 더 빠를지는 확신할 수 없습니다. GPU의 메모리 접근 방식이나 셰이더 실행 방식은 기기마다 다르기 때문에, 특정 GPU에서는 기존 방식이 더 효율적일 수도 있습니다. 그러나 현재 테스트 결과로는, 이 최적화가 특히 큰 외곽선 반경에서 효과적인 것으로 보입니다.
Downsample
There is one more “easy” optimization. Like the Gaussian blur approach this technique lends itself well to relatively easy downsampling. For very wide outlines or higher resolutions it wouldn’t be too difficult to render the starting mask at a lower resolution, or downsample it for better quality, and run the JFA at that lower resolution. Especially with the added sub pixel estimation in the initialize pass. I did actually try this and it can really significantly improve performance as you would expect.
But also like the Gaussian blur it means some of the details get smoothed out. There’s also a gotcha with the final outline pass. You can’t just use bilinear sampling on the output from the jump flood passes as it’s interpolating an offset position. This produces very weird artifacts in any interior corners. So instead you need to add one more pass to decode the distance field to a texture for the final outline pass to sample from. And even then you may want to add some kind of higher quality bicubic or catmull-rom filtering to hide the linear artifacts of bilinear filtering. I don’t implement this. Might be a good option for supporting very high resolutions more easily.
다운샘플링
“쉬운” 최적화가 하나 더 있습니다. 가우시안 블러 접근 방식처럼 이 기술도 비교적 쉬운 다운샘플링에 잘 맞습니다. 매우 넓은 외곽선이나 높은 해상도에서는 시작 마스크를 낮은 해상도로 렌더링하거나 품질을 높이기 위해 다운샘플링하여 JFA를 낮은 해상도에서 실행하는 것이 그리 어렵지 않을 것입니다. 특히 초기화 패스에서 서브 픽셀 추정을 추가하면 더욱 그렇습니다. 실제로 이를 시도해 보았고, 예상대로 성능을 크게 개선할 수 있었습니다.
하지만 가우시안 블러처럼 디테일이 일부 부드럽게 처리된다는 단점이 있습니다. 최종 외곽선 패스에서도 주의할 점이 있습니다. 점프 플러드 패스의 출력에 대해 단순히 선형 샘플링(bilinear sampling)을 사용할 수는 없습니다. 이는 오프셋 위치를 보간하므로 내부 코너에서 매우 이상한 아티팩트를 발생시킵니다. 따라서 최종 외곽선 패스가 샘플링할 수 있도록 거리 필드를 텍스처로 디코딩하는 추가 패스를 하나 더 추가해야 합니다. 그리고 나서도, 선형 보간의 아티팩트를 숨기기 위해 더 높은 품질의 비큐빅(bicubic) 또는 Catmull-Rom 필터링을 추가하는 것이 좋을 수도 있습니다. 저는 이를 구현하지 않았습니다. 하지만 아주 높은 해상도를 더 쉽게 지원하기 위한 좋은 옵션이 될 수 있습니다.
Compute
A compute shader would likely be faster at this than the render texture approach I’m currently using. But that’s a task for another day.
컴퓨트
현재 사용 중인 렌더 텍스처 방식보다 컴퓨트 셰이더가 이 작업을 더 빠르게 처리할 가능성이 높습니다. 하지만 그것은 나중에 할 과제입니다.
Final Words
So, obviously I failed at making a brute force outline that could compete with a more efficient approach. But I hope you enjoyed reading about my trip as much as I did. And now we have a much more efficient, and more adaptable outline technique. Mainly because a the jump flood based approach can do so much more. For example you could use a gradient instead of a simple edge. Even an animated gradient if you really want to be fancy.
마지막 한마디
분명히 저는 더 효율적인 접근 방식과 경쟁할 수 있는 브루트 포스 외곽선을 만드는 데 실패했습니다. 하지만 제가 겪은 과정을 읽는 것이 저만큼이나 즐거우셨기를 바랍니다. 그리고 이제 우리는 훨씬 더 효율적이고, 더 적응력 있는 외곽선 기술을 갖게 되었습니다. 주로 점프 플러드 기반 접근 방식이 훨씬 더 많은 것을 할 수 있기 때문입니다. 예를 들어, 단순한 가장자리 대신 그라디언트를 사용할 수도 있습니다. 정말 멋을 부리고 싶다면 애니메이션 그라디언트도 사용할 수 있습니다.
You could also do interesting things like render out a depth texture and composite the outline into the scene with the depth of the closest edge! But I’ll leave you to play with that.
깊이 텍스처(depth texture)를 렌더링하고, 가장 가까운 가장자리의 깊이 값을 사용하여 외곽선을 장면에 합성하는 것과 같은 흥미로운 작업도 할 수 있습니다! 하지만 그것은 여러분이 직접 시도해 보시길 바랍니다.

Additional Thoughts
After posting this I got a couple of questions and comments on the article I want to address.
추가적인 생각들
이 글을 게시한 후, 몇 가지 질문과 댓글을 받았는데, 이에 대해 답변하고자 합니다.
Geometry Shaders
I’ve had a couple of people ask about or even show their geometry shader options. I’m not a fan of these for various reasons. There are several very convincing academic articles on using geometry shaders to do very high quality outlines, but they all require adjacency data. That’s literally having each triangle know the vertices of its adjacent triangles. No real time engine I’m aware of actually supports this. And even if it did it still requires the mesh to have no seams. The easier and still effective method is to generate outline geometry on every single triangle of the mesh, but this requires either some amount of geometry processing similar to the vertex push method, and/or an extreme amount overdraw.
지오메트리 셰이더
몇몇 사람들이 지오메트리 셰이더 옵션에 대해 물어보거나 자신들의 방법을 보여주기도 했습니다. 저는 여러 가지 이유로 지오메트리 셰이더를 선호하지 않습니다.
지오메트리 셰이더를 사용해 매우 높은 품질의 외곽선을 생성하는 몇 가지 매우 설득력 있는 학술 논문들이 있지만, 이 방법들은 모두 **인접 데이터(adjacency data)**를 요구합니다. 즉, 각 삼각형이 자신의 인접 삼각형의 정점을 알아야 한다는 의미입니다. 제가 아는 한, 어떤 실시간 엔진도 이를 실제로 지원하지 않습니다.
설사 지원한다고 해도, 이 방법은 메시(mesh)에 이음새(seams)가 없어야 한다는 추가 요구 사항이 따릅니다. 좀 더 간단하면서도 여전히 효과적인 방법은 메시의 모든 삼각형에 대해 외곽선 지오메트리를 생성하는 것입니다. 그러나 이 방식은 버텍스 푸시(vertex push) 방법과 유사한 어느 정도의 지오메트리 처리가 필요하거나, 극도로 많은 오버드로우(overdraw)를 발생시킬 수 있습니다.
In the end they end up being way worse for performance than something like the vertex push method, with only minor improvements. It’d be interesting to compare them at some point as it is possible to generate accurate distance fields on arbitrary geometry with a version of this technique.
결국, 지오메트리 셰이더는 성능 면에서 버텍스 푸시(vertex push) 방식보다 훨씬 나쁘며, 개선 효과는 미미한 수준에 그칩니다. 그러나 이 기법의 변형을 사용하여 임의의 기하학적 구조에서 정확한 거리 필드를 생성할 수 있기 때문에, 이를 어느 시점에서 비교해 보는 것은 흥미로울 것입니다.
An Outline of an Outline
이것은 훌륭한 제안입니다. 이 방법도 작동하며, 브루트 포스 방식을 가우시안 블러 접근 방식과 동일한 선형 외곽선 두께 대비 비용 수준으로 맞출 수 있을 것입니다. 어쩌면 더 나은 결과를 얻을 수도 있습니다! 정말 재미있는 시도가 될 것입니다.
매번 mip 체인을 재생성할 필요는 없겠지만, 각 패스마다 스텐실을 초기화하고 다시 처리해야 할 것입니다. 또한, 작은 오류가 누적될 가능성도 염려됩니다.
그렇다 해도 JFA에는 여전히 미치지 못할 것입니다.
Outlined Sprites
One nice advantage all of the image based outline techniques have over geometry based approaches is they can work on objects that have their edge set by a texture rather than geometry. Like a sprite or any transparent material. It’s as “simple” as rendering to the silhouette texture with alpha instead of as solid geometry. The big caveat is only the brute force methods will work properly with any kind of soft alpha. And even that will work better if you hard edge. Indeed the JFA can only support hard edges. So you’d need to render to the silhouette texture using alpha test, or better yet a sharpened alpha blend or alpha to coverage, like I detailed in my alpha to coverage article.
외곽선이 있는 스프라이트
이미지 기반 외곽선 기법이 지오메트리 기반 접근 방식에 비해 가지는 장점 중 하나는, 기하학이 아니라 텍스처로 가장자리가 정의된 객체에서도 작동한다는 점입니다. 예를 들어, 스프라이트(sprite)나 투명 재질을 사용하는 객체 같은 경우입니다. 이 작업은 실루엣 텍스처를 단색 기하학으로 렌더링하는 대신 알파로 렌더링하는 것만큼 "간단"합니다.
하지만 큰 주의점은, 소프트 알파를 사용하는 경우 제대로 작동하는 것은 브루트 포스 방식뿐이라는 점입니다. 그마저도 하드 엣지(hard edge)를 사용하면 더 나은 결과를 얻을 수 있습니다. 실제로 JFA는 하드 엣지만 지원할 수 있습니다. 따라서 실루엣 텍스처로 렌더링할 때 **알파 테스트(alpha test)**를 사용하거나, 더 나은 방법으로는 **강화된 알파 블렌드(sharpened alpha blend)**나 **알파 투 커버리지(alpha to coverage)**를 사용하는 것이 필요합니다. 이 방법에 대해서는 제 알파 투 커버리지 글에서 자세히 설명한 바 있습니다.
https://bgolus.medium.com/anti-aliased-alpha-test-the-esoteric-alpha-to-coverage-8b177335ae4f
Anti-aliased Alpha Test: The Esoteric Alpha To Coverage
Aliasing is the bane of VR. We have several tools we use to try to remove, or at least reduce aliasing in real time graphics today. Tools…
bgolus.medium.com
The Sobel based JFA initialization in the implementation example expects any kind of anti-aliasing to be no more than a single pixel edge, otherwise the estimation will fail.
소벨(Sobel) 기반 JFA 초기화는 구현 예제에서 안티앨리어싱이 한 픽셀 가장자리(싱글 픽셀 엣지)를 넘지 않아야 제대로 작동합니다. 그렇지 않으면 추정 과정이 실패하게 됩니다.
Real Numbers
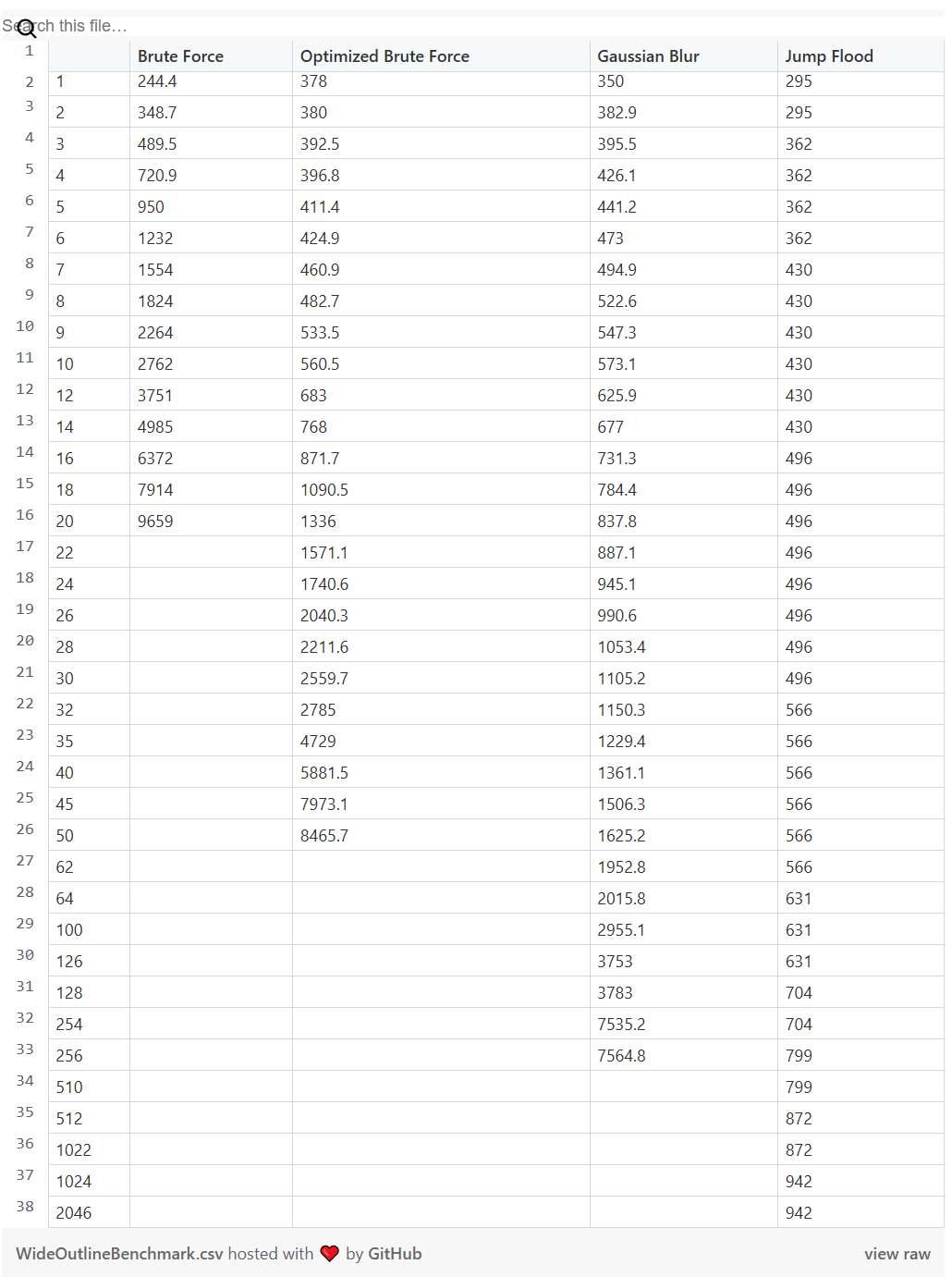
Here’s the raw table of numbers I used to generate the graphs above. I don’t remember if the numbers for the straight brute force are using a stencil for the interior mask or resampling the original silhouette. Optimized brute force and Gaussian blur are as described above. Jump flood numbers are all the same for each “jump” in radius, not because that’s how they actually benchmarked, but because I had rerun this several times as I was tweaking it and started getting lazy. Plus I knew from previous runs the number didn’t change meaningfully within each radius jump, and because the fractional values weren’t visible in the graph.
실제 숫자
아래는 위의 그래프를 생성하는 데 사용한 원본 데이터입니다. 직선 브루트 포스 방식에 대한 숫자가 내부 마스크를 위한 스텐실을 사용하는지, 원래의 실루엣을 다시 샘플링(resampling)하는지 기억이 나지 않습니다. 최적화된 브루트 포스와 가우시안 블러는 위에서 설명한 대로입니다.
점프 플러드(Jump Flood) 방식의 숫자는 각 반경 "점프"에서 동일하게 보이는데, 이는 실제 벤치마크 결과가 그렇다는 뜻이 아니라, 제가 여러 번 조정을 하면서 다시 실행해 보았기 때문입니다. 그러다 보니 조금 게을러져서 숫자를 그대로 둔 것입니다. 게다가 이전 실행 결과로부터 반경 점프 내에서 숫자가 의미 있게 변하지 않는다는 것을 이미 알고 있었고, 소수점 값은 그래프에서 보이지 않으므로 큰 영향을 주지 않았습니다.
Left column is the pixel radius. All numbers are in microseconds, not milliseconds.
픽셀 반경은 왼쪽 열에 있습니다. 모든 숫자는 마이크로초(μs) 단위입니다. **밀리초(ms)**가 아님을 유의하세요.
Code Samples
Here is example code for the final anti-aliased jump flood outline effect.
(direct link to gist.)
코드 샘플
다음은 최종 안티앨리어싱 점프 플러드 외곽선 효과를 위한 예제 코드입니다.
https://gist.github.com/bgolus/a18c1a3fc9af2d73cc19169a809eb195
Jump flood based outline effect for Unity https://medium.com/@bgolus/the-quest-for-very-wide-outlines-ba82ed442cd9
Jump flood based outline effect for Unity https://medium.com/@bgolus/the-quest-for-very-wide-outlines-ba82ed442cd9 - HiddenJumpFloodOutline.shader
gist.github.com
'유니티3D > 셰이더' 카테고리의 다른 글
| 유니티로 게임 제작 기법 연습 - UI용 셰이더 만들기 (0) | 2024.11.18 |
|---|---|
| 유니티로 게임 제작 기법 연습01 - 유니티 라이팅 셰이더 바닥부터 구현하기 (2) | 2024.11.11 |